题目内容
14.某足球协会举办了一次足球联赛,其记分规定及奖励方案如下表:| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金(元/人) | 1300 | 500 | 0 |
(1)试说明w是否能等于11400元.
(2)通过计算,判断A队胜、平、负各几场,并说明w可能的最大值.
分析 (1)设A队胜x场,平y场.根据题意列出关于x、y的方程组,求出xy的值,进而可得出结论;
(2)由3x+y=17,得y=17-3x,再分x=3、4、5三种情况进行讨论.
解答 解:设A队胜x场,平y场
(1)由题意得:$\left\{\begin{array}{l}3x+y=17\\ 1300x+500y+11×300=11400\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=2\\ y=11\end{array}\right.$.
因为x+y=2+11=13,即胜2场,平11场与总共比赛11场不符,故w不能等于11400元.
(2)由3x+y=17,得y=17-3x
所以只能有下三种情况:
①当x=3时,y=8,即胜3场,平8场,负0场;
②当x=4时,y=5,即胜4场,平5场,负2场;
③当x=5时,y=2,即胜5场,平2场,负4场.
又w=1300x+500y+3300
将y=17-3x代入得:w=-200x+11800
易知:当x=3时,w最大=-200×3+11800=11200(元).
点评 本题考查的是一次函数的应用,在解答(2)时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
4.直角三角形的两直角边分别为a,b,斜边为c,则下列关于a,b,c三边的关系式不正确的是( )
| A. | b2=c2-a2 | B. | a2=c2-b2 | C. | b2=a2-c2 | D. | c2=a2+b2 |
2.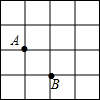 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )| A. | $\frac{6}{25}$ | B. | $\frac{1}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{7}{25}$ |
19.已知某同学近几次的数学成绩(单位:分)分别为92,90,88,92,93,则该同学这几次数学成绩的平均数和众数分别是( )
| A. | 90分,90分 | B. | 91分,92分 | C. | 92分,92分 | D. | 89分,92分 |
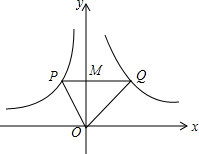 如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3.
如图,点P(-1,2)、Q(2,2)分别位于两个不同的双曲线上,则S△POQ=3. 如图,BE,CF分别是△ABC的两条高且相交于点D.
如图,BE,CF分别是△ABC的两条高且相交于点D.