题目内容
9.(1)计算:($\frac{1}{3}$)-2+$\root{3}{-8}$-|-5|+($\sqrt{3}$-2)0(2)先化简$(1-\frac{2}{a+1})÷\frac{{{a^2}-2a+1}}{{{a^2}+a}}$,再从$\sqrt{2a-1}$有意义的范围内选取一个整数作为a的值代入求值.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用立方根定义计算,第三项利用绝对值的代数意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a=2代入计算即可求出值.
解答 解:(1)原式=9+(-2)-5+1=3;
(2)原式=$\frac{a-1}{a+1}$•$\frac{a(a+1)}{(a-1)^{2}}$=$\frac{a}{a-1}$,
∵$\sqrt{2a-1}$有意义,
∴2a-1≥0,即a≥$\frac{1}{2}$,
则当a=2时,原式=$\frac{2}{2-1}$=2.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
19.如图,∠APB是圆周角的是( )
| A. |  | B. |  | C. |  | D. |  |
14.某足球协会举办了一次足球联赛,其记分规定及奖励方案如下表:
当比赛进行到第11轮结束(每队均须比赛11场)时,A队共积17分,每赛一场,每名参赛队员均得出场费300元.设A队其中一名参赛队员所得的奖金与出场费的和为w(元).
(1)试说明w是否能等于11400元.
(2)通过计算,判断A队胜、平、负各几场,并说明w可能的最大值.
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金(元/人) | 1300 | 500 | 0 |
(1)试说明w是否能等于11400元.
(2)通过计算,判断A队胜、平、负各几场,并说明w可能的最大值.
1.下列命题是真命题的是( )
| A. | 任何数的0次幂都等于1 | |
| B. | 顺次连接菱形四边中点的线段组成的四边形是正方形 | |
| C. | 图形的旋转和平移会改变图形的形状和大小 | |
| D. | 角平分线上的点到角两边的距离相等 |
 已知:如图所示,AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠D0E=60°,求∠C的度数.
已知:如图所示,AB为⊙O的直径,C是⊙O外一点,BC交⊙O于点E,AC交⊙O于点D,∠D0E=60°,求∠C的度数.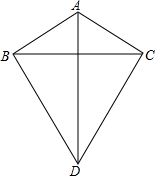 如图所示,四边形ABDC中,AD同时平分∠BAC和∠BDC,问:B,C两点是否关于直线AD对称?请证明.
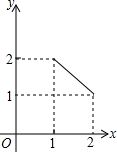
如图所示,四边形ABDC中,AD同时平分∠BAC和∠BDC,问:B,C两点是否关于直线AD对称?请证明.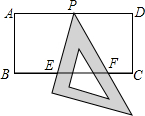 如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )
如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )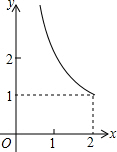
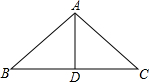 如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.
如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.