题目内容
4．直角三角形的两直角边分别为a，b，斜边为c，则下列关于a，b，c三边的关系式不正确的是（ ）| A． | b2=c2-a2 | B． | a2=c2-b2 | C． | b2=a2-c2 | D． | c2=a2+b2 |
分析 直接利用勾股定理分别分析得出答案．
解答 解：∵直角三角形的两直角边为a，b，斜边为c，
∴a2+b2=c2，
故选项A正确，不合题意；
∵b2=c2-a2，∴a2+b2=c2，
故选项B正确，不合题意；
∵b2=a2-c2，∴c2+b2=a2，
故选项C不正确，符合题意；
故选：C．
点评 此题主要考查了勾股定理，正确利用等式的基本性质得出是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
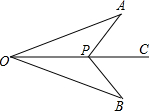如图，点P是∠AOB的角平分线OC上一点，分别连接AP、BP，若再添加一个条件即可判定△AOP≌△BPO，则一下条件中：①∠A=∠B；②∠APO=∠BPO；③∠APC=∠BPC； ④AP=BP；⑤OA=OB．其中一定正确的是①②③⑤（只需填序号即可）
如图，AB，CD为⊙O的两条直径，E，F分别为OA，OB的中点，求证：四边形CEDF为平行四边形．
19．如图，∠APB是圆周角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
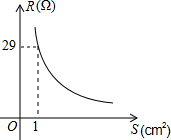实验表明，当导线的长度一定时，导线的电阻与它的横截面积成反比例，一条长为100km的铅导线的电阻R（Ω）与它的横截面积S（cm2）的函数图象如图所示，那么，其函数关系式为R=$\frac{29}{S}$；当S=2cm2时，R=14.5Ω．
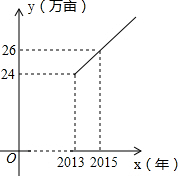某市实施“农业立市，工业强市，旅游兴市”计划后，2013年全市荔枝种植面积为24万亩．调查分析结果显示：从2013年开始，该市荔枝种植面积y（万亩）随着时间x（年）逐年成直线上升，y与x之间的函数关系如图所示．
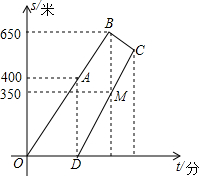小明要在周日8点50分之前赶到距家1000米的书店去买书．早8点20分从家出发，8分钟后妈妈发现他忘了带钱包，于是立即出发按他走的路线去追．妈妈出发几分钟后，小明也发现了忘带钱包，于是按原路原速返回去取，几分钟后与妈妈相遇．假设在此过程中小明和妈妈的速度均保持不变，如图所示，给出两人离家距离s（米）和小明所走的时间t（分）之间的函数图象，结合图象回答下列问题：
14．某足球协会举办了一次足球联赛，其记分规定及奖励方案如下表：
当比赛进行到第11轮结束（每队均须比赛11场）时，A队共积17分，每赛一场，每名参赛队员均得出场费300元．设A队其中一名参赛队员所得的奖金与出场费的和为w（元）．
（1）试说明w是否能等于11400元．
（2）通过计算，判断A队胜、平、负各几场，并说明w可能的最大值．
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金（元/人） | 1300 | 500 | 0 |
（1）试说明w是否能等于11400元．
（2）通过计算，判断A队胜、平、负各几场，并说明w可能的最大值．