Question

9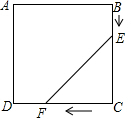．如图，甲、乙两车分别从正方形广场ABCD的顶点B，C两点同时出发，甲由C向D运动，乙由B向C运动，甲的速度为1千米/分，乙的速度为2千米/分，若正方形广场的周长为40km．
（1）几分钟后两车相距2$\sqrt{10}$km？
（2）△CEF的面积能否等于7km²，说明理由．

Answer 1

分析 （1）本题可设时间为x分钟，依题意得CF=x，则BE=2x，周长为40km，边长为10km，CE=10-2x，利用勾股定理列方程求解；
（2）根据题意列方程得到此方程无实数根，于是得到结论．

解答 解：（1）设x分钟后两车相距2×$\sqrt{10}$km，
此时甲运动到F点，乙运动到E点，
可知：FC=x，EC=10-2x，
在Rt△ECF中，x²+（10-2x）²=（2$\sqrt{10}$）²，
解得：x₁=2，x₂=6，
当x=2时，FC=2，EC=10-4=6＜10符合题意，
当x=6时，FC=6，EC=10-12=-2＜0不符合题意，舍去，
答：2分钟后，两车相距2$\sqrt{10}$千米；

（2）△CEF的面积不能等于7km²．
设t分钟后△CEF的面积等于7km²，
∵甲的速度为1千米/分，乙的速度为2千米/分，
∴CF=t，CE=10-2t，
∴$\frac{1}{2}$•t•（10-2t）=7，
整理得：t²-5t+7=0，
∵△=（-5）²-4×7＜0，
∴此方程无实数根，
∴△CEF的面积不能等于7km²．

点评 此题考查了一元二次方程的应用和勾股定理的应用，根据路程=速度×时间，表示线段的长度，将问题转化到三角形中，利用勾股定理或者面积关系建立等量关系，是解应用题常用的方法．