题目内容
18. 如图所示,已知∠1+∠2=180°,∠B=∠3,DE和BC平行吗?如果平行,请说明理由.
如图所示,已知∠1+∠2=180°,∠B=∠3,DE和BC平行吗?如果平行,请说明理由.
分析 由条件可得到∠2+∠4=180°可证得AB∥EH,可得到∠3+∠BDE=180°,结合条件可证明DE∥BC.
解答 解;DE∥BC,理由如下:
∵∠1+∠2=180°,∠1=∠DFH,
∴∠2+∠DFH=180°,
∴AB∥EH,
∴∠3+∠BDE=180°,
∵∠B=∠3,
∴∠B+∠BDE=180°,
∴DE∥BC.
点评 本题主要考查平行线的判定,用到的知识点为:同旁内角互补,两直线平行.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6. 如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
 如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
3.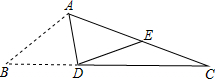 如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
 如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )| A. | 80° | B. | 60° | C. | 40° | D. | 30° |
10.-64的立方根是( )
| A. | -4 | B. | 8 | C. | -4和4 | D. | -8和8 |
7.下列命题中是真命题的是( )
| A. | 确定性事件发生的概率为1 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 正n边形都是轴对称图形,并且有n条对称轴 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
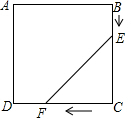 如图,甲、乙两车分别从正方形广场ABCD的顶点B,C两点同时出发,甲由C向D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场的周长为40km.
如图,甲、乙两车分别从正方形广场ABCD的顶点B,C两点同时出发,甲由C向D运动,乙由B向C运动,甲的速度为1千米/分,乙的速度为2千米/分,若正方形广场的周长为40km.