题目内容
(1)解不等式组:
(2)化简:(
-
)÷
.
|
(2)化简:(
| 2x |
| x+2 |
| x |
| x-2 |
| x |
| x2-4 |
考点:解一元一次不等式组,分式的混合运算
专题:
分析:(1)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(2)首先把括号内的分式进行通分、相减,把除法转化为乘法,然后对分式进行化简即可.
(2)首先把括号内的分式进行通分、相减,把除法转化为乘法,然后对分式进行化简即可.
解答:解:(1)
,
解①得:x≥-1,
解②得:x<3,
则不等式的解集是:-1≤x<3;
(2)原式=
•
=
=2(x-2)-(x+2)
=2x-4-x-2
=x-6.
|
解①得:x≥-1,
解②得:x<3,
则不等式的解集是:-1≤x<3;
(2)原式=
| 2x(x-2)-x(x+2) |
| (x+2)(x-2) |
| (x+2)(x-2) |
| x |
=
| 2x(x-2)-x(x+2) |
| x |
=2(x-2)-(x+2)
=2x-4-x-2
=x-6.
点评:本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若不等式x<3的解都能使关于x的一次不等式(a-1)x<a+3成立,则a的取值范围是( )
| A、1<a<3 |
| B、a<1或a>3 |
| C、1≤a<3 |
| D、1<a≤3 |
某商品原价500元,连续两次降价a%后售价为200元,下列所列方程正确的是( )
| A、500(1+a%)2=200 |
| B、500(1-a2%)=200 |
| C、500(1-2a%)=200 |
| D、500(1-a%)2=200 |
 如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数)
如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数)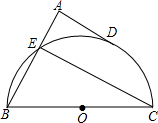 如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、
如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、