题目内容
2．解不等式组$\left\{\begin{array}{l}\frac{x-3}{4}+6≥x\\ 4-5（{x-2}）＜8-2x\end{array}\right.$，并求其整数解．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式$\frac{x-3}{4}$+6≥x，得：x≤7，
解不等式4-5（x-2）＜8-2x，得：x＞2，
∴不等式组的解集为2＜x≤7．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
如图，已知AB∥DE，D是BC的中点，∠A=∠E，证明：△ABD≌△EDC．
13．一个三角形的周长为7cm，一边长为3cm，其中有两条边的长度相等，则这个三角形的各边长是（ ）
| A． | 3 cm，2 cm，2 cm | |
| B． | 3 cm，1 cm，3 cm | |
| C． | 3 cm，2 cm，2 cm和3 cm，1 cm，3 cm都有可能 | |
| D． | 不能确定 |
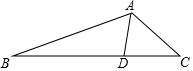如图，在△ABC中，AB=6，AC=4，∠BAC=120°，∠BAC的平分线交BC于点D，则AD=$\frac{12}{5}$．