题目内容
如图，在△ACB中，D为AC边上的中点，AE∥BC，ED交AB于G，交BC的延长线于F，若BG：GA=3：1，CB=4，则AE的长为考点：相似三角形的判定与性质
专题：
分析：首先证明△AED∽△CFD，列出比例式，结合AD=DC，得到AE=CF；证明△AEG∽△BFG，结合BG：GA=3：1，得到BF=3AE，即可解决问题．
解答：解：∵D为AC边上的中点，AE∥BC，
∴△AED∽△CFD，AD=DC；
∴
=
，AE=CF（设为λ）；
∵AE∥BC，
∴△AEG∽△BFG，
∴
=
，
∵BG：GA=3：1，
∴BF=3AE，即BC+λ=3λ，
∴λ=
BC=2，即AE的长为2．
故答案为2．
解：∵D为AC边上的中点，AE∥BC，∴△AED∽△CFD，AD=DC；
∴
| AE |
| CF |
| AD |
| DC |
∵AE∥BC，
∴△AEG∽△BFG，
∴
| BF |
| AE |
| BG |
| AG |
∵BG：GA=3：1，
∴BF=3AE，即BC+λ=3λ，
∴λ=
| 1 |
| 2 |
故答案为2．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是牢固掌握相似三角形的判定及其性质，这是灵活运用解题的基础和关键．
练习册系列答案
相关题目
读语句作图
如图，△AOB≌△ADC，点B和点C是对应顶点，∠O=∠D=90°，记∠OAD=α，∠ABO=β，当BC∥OA时，α与β之间的数量关系为（ ）| A、α=β |
| B、α=2β |
| C、α+β=90° |
| D、α+2β=180° |
如图，直线AB、CD相交于点O，OD平分∠BOE，OF平分∠AOE，则∠AOF的余角的个数为（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
如图，已知在△ABC中，∠ACB=90°，点D在边BC上，CE⊥AB，CF⊥AD，E、F分别是垂足．
如图，观察海岛（AB），立两标杆（CD，EF），并使点F，D，B在同一直线上，两标杆前后相距1000步，标杆均高3丈，若从标杆CD后退123步，观察者的眼睛H（靠近地面）与标杆顶端C，岛的峰顶A在同一直线上；从标杆EF后退127步，同样观察者的眼睛K（靠近地面）与标杆顶端E，岛的峰顶A在同一直线上；问海岛的峰高AB和海岛离标杆CD的距离BD分别为多少？（注：1步=6尺，1丈=10尺）
如图，直线AB、CD相交于点O，过点O作两条射线OM、ON，且∠AOM=∠CON=90°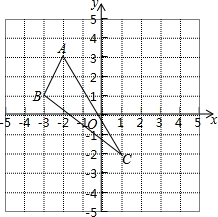
在平面直角坐标系中，△ABC的三个顶点位置如图所示．