题目内容
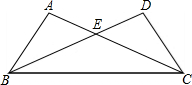 如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌△DCE;
(2)若∠AEB=40°,求∠EBC的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)根据已知条件和图形中隐藏的条件对顶角相等即可证明:△ABE≌△DCE;
(2)由(1)可知BE=CE,所以△BEC是等腰三角形,由等腰三角形的性质和三角形的外角和定理即可求出∠EBC的度数.
(2)由(1)可知BE=CE,所以△BEC是等腰三角形,由等腰三角形的性质和三角形的外角和定理即可求出∠EBC的度数.
解答:解:(1)在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
(2)∵△ABE≌△DCE,
∴BE=CE,
∴∠EBC=∠ECB,
∵∠AEB=40°,
∴∠EBC=20°.
|
∴△ABE≌△DCE(AAS);
(2)∵△ABE≌△DCE,
∴BE=CE,
∴∠EBC=∠ECB,
∵∠AEB=40°,
∴∠EBC=20°.
点评:本题考查了全等三角形的判定和性质以及等腰三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
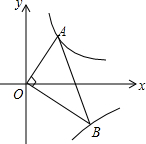 如图,已知,第一象限内的点A在反比例函数y=
如图,已知,第一象限内的点A在反比例函数y=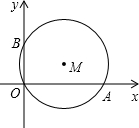 如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.
如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.