题目内容
(1)计算:①(2
+3
)(
-
);②(3
-2
+
)÷2
;
(2)在实数范围内分解因式:①?9a4-25;②a4-4a2+4.
| 3 |
| 2 |
| 2 |
| 3 |
| 12 |
|
| 48 |
| 3 |
(2)在实数范围内分解因式:①?9a4-25;②a4-4a2+4.
考点:二次根式的混合运算,实数范围内分解因式
专题:计算题
分析:(1)①利用多项式乘法公式展开,然后合并即可;
②先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(2)①先提9,再利用平方差公式分解得到原式=9(a2-
)(a2+
),然后再利用平方差公式分解即可;
②先利用完全平方公式分解,然后利用平方差公式分解.
②先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(2)①先提9,再利用平方差公式分解得到原式=9(a2-
| 5 |
| 3 |
| 5 |
| 3 |
②先利用完全平方公式分解,然后利用平方差公式分解.
解答:解:(1)①原式=2
-6+12-3
=6-
;
②原式=(6
-
+4
)÷2
=
÷2
=
;
(2)①原式=9(a2-
)(a2+
)
=9(a+
)(a-
)(a2+
);
②原式=(a2-2)2
=[(a+
)(a-
)]2
=(a+
)2(a-
)2.
| 6 |
| 6 |
=6-
| 6 |
②原式=(6
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
=
28
| ||
| 3 |
| 3 |
=
| 14 |
| 3 |
(2)①原式=9(a2-
| 5 |
| 3 |
| 5 |
| 3 |
=9(a+
| ||
| 3 |
| ||
| 3 |
| 5 |
| 3 |
②原式=(a2-2)2
=[(a+
| 2 |
| 2 |
=(a+
| 2 |
| 2 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了在实数范围内因式分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
实数16的平方根是( )
| A、-2 | B、4 | C、±2 | D、±4 |
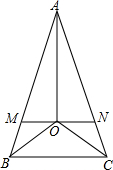 如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.
如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.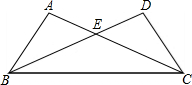 如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 如图,在△ABC中,∠B=2∠C,∠BAC的角平分线交BC于D.
如图,在△ABC中,∠B=2∠C,∠BAC的角平分线交BC于D. 如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数;若∠C=α,求∠D的度数.
如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数;若∠C=α,求∠D的度数.