题目内容
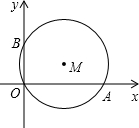 如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.
如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD•CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似?若存在,直接写出点C的坐标;若不存在,请说明理由.
考点:圆的综合题
专题:综合题
分析:(1)利用因式分解法解方程即可得到OA=12,OB=5;
(2)连接AB、AC、MC,MC与OA交于F,如图1,由OC2=CD•CB,∠OCD=∠BCO,根据相似三角形的判定方法即可得到△COD∽△CBO,则∠2=∠1,而根据圆周角定理有∠1=∠3,所以∠2=∠3,得到弧AC=弧OC,根据垂径定理得MC⊥OA,OF=AF=
OA=6,然后根据圆周角定理由∠AOB=90°得AB为⊙M的直径,则在Rt△AOB中,根据勾股定理可计算出AB=13,得到MC=
,易得MF=
OB=
,则FC=MC-MF=4,于是得到C点坐标为(6,-4);
(3)连接AC,连接CM并延长交OA于F,如图2,若CA=CO,则∠COA=∠CAO,根据邻补角的定义得∠COA+∠COD=180°,根据圆内接四边形的性质得∠CAO+∠CBO=180°,则∠COD=∠CBO,加上∠OCD=∠DCO,根据相似的判定方法即可得到△CBO∽△COD;由CA=CO得弧CA=弧CO,根据垂径定理得CF⊥AC,由(2)得MF=
,CM=
,OF=6,则CF=CM+MF=9,于是得到C点坐标为(6,9).
(2)连接AB、AC、MC,MC与OA交于F,如图1,由OC2=CD•CB,∠OCD=∠BCO,根据相似三角形的判定方法即可得到△COD∽△CBO,则∠2=∠1,而根据圆周角定理有∠1=∠3,所以∠2=∠3,得到弧AC=弧OC,根据垂径定理得MC⊥OA,OF=AF=
| 1 |
| 2 |
| 13 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
(3)连接AC,连接CM并延长交OA于F,如图2,若CA=CO,则∠COA=∠CAO,根据邻补角的定义得∠COA+∠COD=180°,根据圆内接四边形的性质得∠CAO+∠CBO=180°,则∠COD=∠CBO,加上∠OCD=∠DCO,根据相似的判定方法即可得到△CBO∽△COD;由CA=CO得弧CA=弧CO,根据垂径定理得CF⊥AC,由(2)得MF=
| 5 |
| 2 |
| 13 |
| 2 |
解答:解:(1)∵(x-12)(x-5)=0,
∴x1=12,x2=5,
∴OA=12,OB=5;
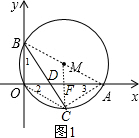 (2)连接AB、AC、MC,MC与OA交于F,如图1,
(2)连接AB、AC、MC,MC与OA交于F,如图1,
∵OC2=CD•CB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠2=∠1,
∵∠1=∠3,
∴∠2=∠3,
∴弧AC=弧OC,
∴MC⊥OA,
∴OF=AF=
OA=6,
∵∠AOB=90°,
∴AB为⊙M的直径,
在Rt△AOB中,OA=12,OB=5,
∴AB=
=13,
∴MC=
,
∵MF为△AOB的中位线,
∴MF=
OB=
,
∴FC=MC-MF=4,
∴C点坐标为(6,-4);
(3)存在.
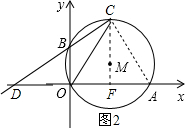 连接AC,连接CM并延长交OA于F,如图2,
连接AC,连接CM并延长交OA于F,如图2,
若CA=CO,则∠COA=∠CAO,
∵∠COA+∠COD=180°,∠CAO+∠CBO=180°,
∴∠COD=∠CBO,
而∠OCD=∠DCO,
∴△CBO∽△COD,
∵CA=CO,
∴弧CA=弧CO,
∴CF⊥AC,
由(2)得MF=
,CM=
,OF=6,
∴CF=CM+MF=9,
∴C点坐标为(6,9).
∴x1=12,x2=5,
∴OA=12,OB=5;
 (2)连接AB、AC、MC,MC与OA交于F,如图1,
(2)连接AB、AC、MC,MC与OA交于F,如图1,∵OC2=CD•CB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠2=∠1,
∵∠1=∠3,
∴∠2=∠3,
∴弧AC=弧OC,
∴MC⊥OA,
∴OF=AF=
| 1 |
| 2 |
∵∠AOB=90°,
∴AB为⊙M的直径,
在Rt△AOB中,OA=12,OB=5,
∴AB=
| OB2+OA2 |
∴MC=
| 13 |
| 2 |
∵MF为△AOB的中位线,
∴MF=
| 1 |
| 2 |
| 5 |
| 2 |
∴FC=MC-MF=4,
∴C点坐标为(6,-4);
(3)存在.
 连接AC,连接CM并延长交OA于F,如图2,
连接AC,连接CM并延长交OA于F,如图2,若CA=CO,则∠COA=∠CAO,
∵∠COA+∠COD=180°,∠CAO+∠CBO=180°,
∴∠COD=∠CBO,
而∠OCD=∠DCO,
∴△CBO∽△COD,
∵CA=CO,
∴弧CA=弧CO,
∴CF⊥AC,
由(2)得MF=
| 5 |
| 2 |
| 13 |
| 2 |
∴CF=CM+MF=9,
∴C点坐标为(6,9).
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理、圆内接四边形的性质和三角形相似的判定与性质;会解一元二次方程和利用勾股定理计算线段的长;理解坐标与图形的性质.

练习册系列答案
相关题目
下列运算中,错误的有( )
①
=1
,②
=±4,③
=2,④
=
+
=
.
①
1
|
| 5 |
| 12 |
| 42 |
| (-2)2 |
|
| 1 |
| 4 |
| 1 |
| 5 |
| 9 |
| 20 |
| A、1个 | B、2个 | C、3个 | D、4个 |
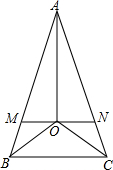 如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.
如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.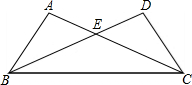 如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 如图,D、E分别在BC、AC边上,且∠B=∠C,AD=DE,∠ADB=∠DEC.
如图,D、E分别在BC、AC边上,且∠B=∠C,AD=DE,∠ADB=∠DEC.