题目内容
12.如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR,设运动时间为t秒,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,则t的值为8-2$\sqrt{7}$秒.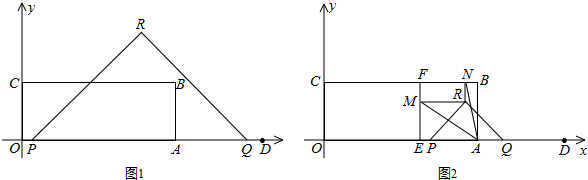
分析 首先判定ABFE为正方形,其次通过旋转,由三角形全等证明MN=EM+BN;设EM=m,BN=n,在Rt△FMN中,由勾股定理得到等式:mn+3(m+n)-9=0,由此等式列方程求出时间t的值.
解答 解:∵E(5,0),
∴AE=AB=3,
∴四边形ABFE是正方形.
如答图2,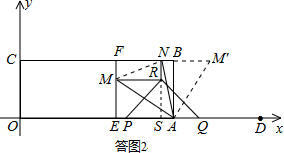
将△AME绕点A顺时针旋转90°,得到△ABM′,其中AE与AB重合,
∵∠MAN=45°,
∴∠EAM+∠NAB=45°,
∴∠BAM′+∠NAB=45°,
∴∠MAN=∠M′AN.
连接MN.
在△MAN与△M′AN中,
$\left\{\begin{array}{l}{AM=AM′}\\{∠MAN=∠M′AN}\\{AN=AN}\end{array}\right.$,
∴△MAN≌△M′AN(SAS),
∴MN=M′N=M′B+BN,
∴MN=EM+BN,
设EM=m,BN=n,则FM=3-m,FN=3-n,
在Rt△FMN中,由勾股定理得:FM2+FN2=MN2,即(3-m)2+(3-n)2=(m+n)2,
整理得:mn+3(m+n)-9=0 ①,
延长NR交x轴于点S,则m=EM=RS=$\frac{1}{2}$PQ=$\frac{1}{2}$(12-3t),
∵QS=$\frac{1}{2}$PQ=$\frac{1}{2}$(12-3t),AQ=4-t,
∴n=BN=AS=QS-AQ=$\frac{1}{2}$(12-3t)-(4-t)=2-$\frac{1}{2}$t,
∴m=3n,
代入①式,化简得:n2+4n-3=0,
解得n=-2+$\sqrt{7}$或n=-2-$\sqrt{7}$(舍去),
∴2-$\frac{1}{2}$t=-2+$\sqrt{7}$,
解得:t=8-2$\sqrt{7}$,
∴若∠MAN=45°,则t的值为(8-2$\sqrt{7}$)秒,
故答案为:8-2$\sqrt{7}$秒.
点评 本题主要考查了全等三角形判定及勾股定理,利用勾股定理求得线段之间的关系式,最后列出方程求解是解答此题的关键.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案

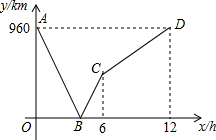 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.
 如图,在平行四边形ABCD中,E是CD中点,AE⊥BE,F是AE中点,FC与BE交于G.求证:AB=2BC.
如图,在平行四边形ABCD中,E是CD中点,AE⊥BE,F是AE中点,FC与BE交于G.求证:AB=2BC.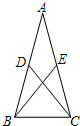 如图,△ABC中,AB=AC,点D、E分别是AB、AC的中点.求证:BE=CD.
如图,△ABC中,AB=AC,点D、E分别是AB、AC的中点.求证:BE=CD.