Question

10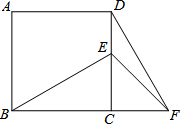．如图，在正方形ABCD中，E为CD边上的一点，F为BC延长线上一点，CE=CF，∠FDC=30°，则∠BEF的度数为105°．

Answer 1

分析 首先证明△BCE≌△DCF，推出∠EBC=∠CDF=30°，求出∠BEC和∠CEF即可解决问题．

解答 解：∵四边形ABCD是正方形，
∴BC=CD，∠BCE=∠DCF=90°，
在△BCE和△DCF中，
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠DCF}\\{CE=CF}\end{array}\right.$，
∴△BCE≌△DCF，
∴∠CBE=∠CDF=30°，
∴∠BEC=60°，
∵CE=CF，∠ECF=90°，
∴∠CEF=∠CFE=45°，
∴∠BEF=∠BEC+∠CEF=105°．

点评 本题考查正方形的性质、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形，属于中考常考题型．