��Ŀ����
20���۲�����ʽ�ӣ���$\sqrt{2-\frac{2}{5}}=2\sqrt{\frac{2}{5}}$����$\sqrt{3-\frac{3}{10}}=3\sqrt{\frac{3}{10}}$����$\sqrt{4-\frac{4}{17}}=4\sqrt{\frac{4}{17}}$����$\sqrt{5-\frac{5}{26}}=5\sqrt{\frac{5}{26}}$�������㰴�չ���д����n��n��1����ʽ���ǣ�������| A�� | $\sqrt{n-1-\frac{n-1}{��n-1��^{2}+1}}$=��n-1��$\sqrt{\frac{n-1}{��n-1��^{2}+1}}$ | B�� | $\sqrt{n-\frac{n}{{n}^{2}-1}}=n\sqrt{\frac{n}{{n}^{2}-1}}$ | ||
| C�� | $\sqrt{n+1-\frac{n+1}{��n+1��^{2}+1}}$=��n+1��$\sqrt{\frac{n+1}{��n+1��^{2}+1}}$ | D�� | $\sqrt{n-\frac{n}{{n}^{2}+1}}=n\sqrt{\frac{n}{{n}^{2}+1}}$ |
���� �۲��ʽ���ҳ����ɣ�д����n��ʽ�Ӽ��ɣ�
��� �⣺�ɹ��ɿɵã���n��ʽ��Ϊ��
$\sqrt{n+1-\frac{n+1}{��n+1��^{2}+1}}$=��n+1��$\sqrt{\frac{n+1}{��n+1��^{2}+1}}$��
��ѡ��B��
���� ������Ҫ����������ƽ����������Ĺؼ��ǹ۲��ʽ���ҳ����ɣ�

��ϰ��ϵ�д�
�����Ŀ
10�����������Ƿ���x2-2x-2=0������ʵ���������2+��2��ֵΪ��������
| A�� | 10 | B�� | 9 | C�� | 8 | D�� | 7 |
11��ij������ӵ���һ��ѡ��һ����Ա���������������������ͬѧ����5��3��Ͷ�����ԣ�ÿ��ÿ��Ͷ10������ͼ��¼����������ͬѧ5��Ͷ������Ͷ�еĸ�����
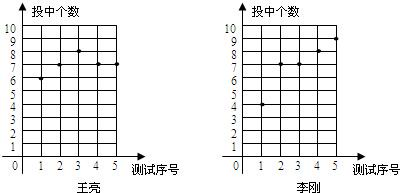
��1���������ͼ�е����ݣ���д����
��2�������ǽ����������ѡ˭����Ҫ˵�����ɣ�

��1���������ͼ�е����ݣ���д����
| ���� | ƽ���� | ���� | ���� |
| ���� | 7 | 7 | 0.4 |
| ��� | 7 | 7 | 2.8 |
8��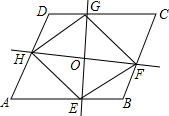 ��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ�������
��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ�������
 ��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ�������
��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ�������| A�� | �٢� | B�� | �٢ڢ� | C�� | �ڢ� | D�� | �ڢۢ� |
5�����㣨m��n���ں���y=2x+1��ͼ���ϣ���4m-2n��ֵ�ǣ�������
| A�� | 2 | B�� | -1 | C�� | 1 | D�� | -2 |
10������������ȷ���ǣ�������
| A�� | ��-3mn��2=-6m2n2 | B�� | 4x4+2x4+x4=6x4 | C�� | ��a-b����-a-b��=a2-b2 | D�� | ��xy��2�£�-xy��=-xy |
 С����һ�������εIJ�����ˤ�����ͼ��ʾ���Ŀ飨��ͼ�б���1��2��3��4���Ŀ飩����ֻ��һ�����ԭ��һ����С�������Σ���Ӧ�ô���2�飮
С����һ�������εIJ�����ˤ�����ͼ��ʾ���Ŀ飨��ͼ�б���1��2��3��4���Ŀ飩����ֻ��һ�����ԭ��һ����С�������Σ���Ӧ�ô���2�飮