题目内容
3.计算:(1)($\sqrt{\frac{8}{3}}-2\sqrt{\frac{5}{12}}$)-$\sqrt{\frac{4}{3}}$
(2)$\sqrt{45}+\sqrt{1\frac{1}{3}}+\sqrt{108}-\sqrt{125}$
(3)9$\sqrt{45}÷3\sqrt{\frac{1}{5}}×\frac{3}{2}\sqrt{2\frac{2}{3}}$
(4)(4$\sqrt{6}-4\sqrt{\frac{1}{2}}+3\sqrt{8}$)$÷2\sqrt{2}$.
分析 (1)(2)先化简二次根式,再进一步合并即可;
(3)按照二次根式的乘除法计算化简;
(4)先化简算加减,再算除法.
解答 解:(1)原式=$\frac{2}{3}$$\sqrt{6}$-$\frac{\sqrt{15}}{3}$-$\frac{2}{3}$$\sqrt{3}$;
(2)原式=3$\sqrt{5}$+$\frac{2}{3}$$\sqrt{3}$+6$\sqrt{3}$-5$\sqrt{5}$
=$\frac{20}{3}$$\sqrt{3}$-2$\sqrt{5}$;
(3)原式=3$\sqrt{225}$×$\sqrt{6}$
=45$\sqrt{6}$;
(4)原式=(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)÷2$\sqrt{2}$
=(4$\sqrt{6}$+4$\sqrt{2}$)÷2$\sqrt{2}$
=$\sqrt{3}$+2.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.计算$(-1)÷\frac{1}{7}×(-7)$的结果为( )
| A. | -49 | B. | 49 | C. | -1 | D. | 1 |
 如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,另一只蚂蚁沿着三个小半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同).
如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,另一只蚂蚁沿着三个小半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同). 如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?
如图,任意画∠O,在∠O的两边上分别截取OA,OB,使OA=OB,过点A画OA的垂线,过点B画OB的垂线,设两条垂线相交于点P,点O在∠APB的平分线上吗?为什么?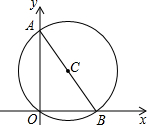 如图,⊙C经过原点O且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,0).
如图,⊙C经过原点O且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,0).
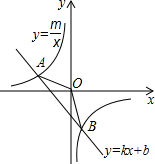 如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2),B(n,-4)是一次函数y1=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;