Question

11．（1）如图1，在△ABC中，AB=AC=BC，点P是AB的中点，D点在CB的延长线上，PC=PD，求证：BC：CD=2：3．
（2）如图2，在△ABC中，AB=AC≠BC，点P是AB的中点，点D在CB的延长线上，PC=PD，结论BC：CD=2：3还成立吗？若成立，请你证明；若不成立，请你求BC：CD的值．

Answer 1

分析 （1）求出∠D=∠BPD=∠PCD=30°，推出DB=PB=$\frac{1}{2}$BC，即可得出答案；
（2）过D作DE∥BC，交AB于E，证△BPD≌△ECP，推出PE=BD=$\frac{1}{2}$BC，即可得出答案．

解答 （1）证明：∵△ABC是等边三角形，
∴∠ABC=∠ACB=60°，AB=AC=BC，
∵点P是AB的中点，
∴∠PCB=30°，AP=PB=$\frac{1}{2}$AB，
∵PD=PC，
∴∠D=∠PCB=30°
∵∠ABC=∠D+∠BPD，
∴∠BPD=30°=∠D，
∴BD=PB=$\frac{1}{2}$AB=$\frac{1}{2}$BC，
∴CD=BD+BC=$\frac{3}{2}$BC，
∴BC：CD=2：3；

（2）成立，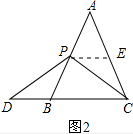
证明：如图2，过D作DE∥BC，交AC于E，
∵点P是AB的中点，
∴E是AC的中点，
∴PE=$\frac{1}{2}$BC，
∵AB=AC，P是AB的中点，E是AC的中点，
∴PB=EC，∠ABC=∠ACB，
∵PD=PC，
∴∠D=∠PCB，
∵∠ABC=∠D+∠BPD，∠ACB=∠PCB+∠PCE，
∴∠BPD=∠PCE，
在△BPD和△ECP中
$\left\{\begin{array}{l}{PD=PC}\\{∠BPD=∠ECP}\\{PB=EC}\end{array}\right.$，
∴△BPD≌△ECP（SAS），
∴DB=PE=$\frac{1}{2}$BC，
∴CD=BD+BC=$\frac{3}{2}$BC，
∴BC：CD=2：3．

点评 本题考查了全等三角形性质和判定，等边三角形性质的应用，题目比较典型，是一道比较好的题目．