题目内容
已知矩形ABCD中,点M是CD上一点,连接AM,作ME⊥AM交射线CB于点E.
①如图1,当CM=BC时,求证AM=ME;
②如图2,若MC:BC=4:3,求sin∠AEM;
③如图3,若AB=5,AD=2,点N是AE的中点,当CM= 时,线段MN有最小值.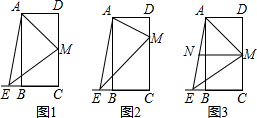
①如图1,当CM=BC时,求证AM=ME;
②如图2,若MC:BC=4:3,求sin∠AEM;
③如图3,若AB=5,AD=2,点N是AE的中点,当CM=

考点:矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)根据CM=BC证得△ADM≌△MCE后即可证得AM=ME;
(2)证得△ADM∽△MCE后即可得到EN:AM=MC:AD=4:3,然后根据∠AME=90°,得到EM:AM:AE=4:3:5,从而求得sin∠AEM的值;
(3)根据MN是直角三角形AME的斜边上的中线可以得MN=
AE,从而得到当AE最小时,MN最小,然后利用相似三角形列出比例式求得CM的值即可.
(2)证得△ADM∽△MCE后即可得到EN:AM=MC:AD=4:3,然后根据∠AME=90°,得到EM:AM:AE=4:3:5,从而求得sin∠AEM的值;
(3)根据MN是直角三角形AME的斜边上的中线可以得MN=
| 1 |
| 2 |
解答:(1)证明:在矩形ABCD中AD=BC,∠D=∠C=90°,
∵BC=CM,
∴CM=AD,
∵∠AME=90°,
∴∠AMD+∠CME=90°,
∵∠AMD+∠DAM=90°,
∴∠CME=∠DAM,
在△ADM与△MCE中,
,
∴△ADM≌△MCE(ASA),
∴AM=EM;
(2)解:在矩形ABCD中AD=BC,∠D=∠C=90°,
∵MC:BC=4:3,
∴MC:AD=4:3,
∵∠AME=90°,
∴∠AMD+∠CME=90°,
∵∠AMD+∠DAM=90°,
∴∠CME=∠DAM,
∴△ADM∽△MCE,
∴EM:AM=MC:AD=4:3,
∵∠AME=90°,
∴EM:AM:AE=4:3:5,
∴sin∠AEM=
;
(3)解:∵∠AME=90°,N为AE的中点,
∴NM=
AE,
∴当AE最小时,MN最小,
∴当AE与AB重合时,AE最小,
∵∠D=∠C,∠AMD=∠MEC,
∴△ADM∽△MCE,
设MC=x,
∵AB=5,AD=2,
∴DM=5-x,
∴
=
解得x=1或4,
故答案为:1或4.
∵BC=CM,
∴CM=AD,
∵∠AME=90°,
∴∠AMD+∠CME=90°,
∵∠AMD+∠DAM=90°,
∴∠CME=∠DAM,
在△ADM与△MCE中,
|
∴△ADM≌△MCE(ASA),
∴AM=EM;
(2)解:在矩形ABCD中AD=BC,∠D=∠C=90°,
∵MC:BC=4:3,
∴MC:AD=4:3,
∵∠AME=90°,
∴∠AMD+∠CME=90°,
∵∠AMD+∠DAM=90°,
∴∠CME=∠DAM,
∴△ADM∽△MCE,
∴EM:AM=MC:AD=4:3,
∵∠AME=90°,
∴EM:AM:AE=4:3:5,
∴sin∠AEM=
| 3 |
| 5 |
(3)解:∵∠AME=90°,N为AE的中点,
∴NM=
| 1 |
| 2 |
∴当AE最小时,MN最小,
∴当AE与AB重合时,AE最小,
∵∠D=∠C,∠AMD=∠MEC,
∴△ADM∽△MCE,
设MC=x,
∵AB=5,AD=2,
∴DM=5-x,
∴
| 2 |
| x |
| 5-x |
| 2 |
解得x=1或4,
故答案为:1或4.
点评:本题考查了矩形的性质、相似及全等的判定与性质,考查的知识点比较多,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
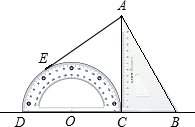 如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则
如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则
 如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,边结DE,OE、OD,求证:DE是⊙O的切线.
如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙O交AB于点D,取AC的中点E,边结DE,OE、OD,求证:DE是⊙O的切线.

 如图,P为直径AB上的一点,点M和N在⊙O上,且∠APM=∠NPB=30°.若OP=2cm,AB=16cm,则PN+PM=
如图,P为直径AB上的一点,点M和N在⊙O上,且∠APM=∠NPB=30°.若OP=2cm,AB=16cm,则PN+PM=