题目内容
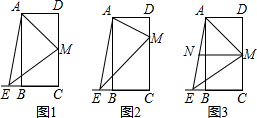
某住宅小区的物业管理部门为解决住户停车困难，将一条道路辟为停车场，停车位置如图所示．已知矩形ABCD是供一辆机动车停放的车位，其中AB=5.4米，BC=2.2米，∠DCF=40°．请计算一辆停车位所占道路的“竖直宽度”EF的大小和“水平宽度”CG的大小（结果精确到0.1米）．参考数据：sin40°≈0.64 cos40°≈0.77 tan40°≈0.84．
考点：解直角三角形的应用
专题：
分析：在直角三角形中，利用三角函数关系，由已知角度和边求得ED和DF，而求得EF的长，再在在Rt△BGC中，利用三角函数关系，求得CG的长．
解答：解：由题意知∠DFC=90°，∠DEA=90°，∠DCF=40°
又∵四边形ABCD是矩形，
∴AB=CD=5.4米，BC=AD=2.2米且∠ADC=90°
∵∠DCF+∠CDF=90°且∠ADE+∠CDF=90°
∴∠DCF=∠ADE=40°，
在Rt△DCF中，sin∠DCF=
，
DF=CDsin∠DCF=5.4×sin40°≈5.4×0.64=3.456米，
在Rt△DAE中，COS∠ADE=
，
DE=AD cos∠ADE=2.2×cos40°≈2.2×0.77=1.694米，
EF=DE+DF≈3.456+1.694=5.2米，
∵AG∥CD，
∴∠BGC=DCF=40°，
在Rt△BGC中，sin∠BGC=
，
CG=
=
=
≈3.4米．
∴停车位所占道路的“竖直宽度”EF约为5.2米，“水平宽度”CG约为3.4米．
又∵四边形ABCD是矩形，
∴AB=CD=5.4米，BC=AD=2.2米且∠ADC=90°
∵∠DCF+∠CDF=90°且∠ADE+∠CDF=90°
∴∠DCF=∠ADE=40°，
在Rt△DCF中，sin∠DCF=
| DF |
| CD |
DF=CDsin∠DCF=5.4×sin40°≈5.4×0.64=3.456米，
在Rt△DAE中，COS∠ADE=
| DE |
| AD |
DE=AD cos∠ADE=2.2×cos40°≈2.2×0.77=1.694米，
EF=DE+DF≈3.456+1.694=5.2米，
∵AG∥CD，
∴∠BGC=DCF=40°，
在Rt△BGC中，sin∠BGC=
| BC |
| CG |
CG=
| BC |
| sin∠BGC |
| BC |
| sin40° |
| 2.2 |
| 0.64 |
∴停车位所占道路的“竖直宽度”EF约为5.2米，“水平宽度”CG约为3.4米．
点评：本题考查了解直角三角形的应用，如何从纷杂的实际问题中整理出直角三角形是解决此类题目的关键．
练习册系列答案
阅读快车系列答案
相关题目
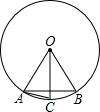如图，在⊙O中，OA=AB，OC⊥AB，则下列结论错误的是（ ）| A、弧AC=弧BC |
| B、△OAB是等边三角形 |
| C、AC=BC |
| D、∠BAC=30° |
周末，甲、乙两组同学从校出发，前往同一景点郊游，甲组同学骑电动车先行，1h后乙组同学乘车前往，图中表示的是甲、乙两组同学各自到达景点的距离s（km）与所用时间t（h）的函数图象，根据已给信息，解答以下问题：