题目内容
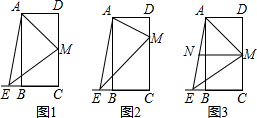
(1)如图(1),△ABC内接于⊙O,AB为直径,∠CAE=∠B,试说明AE与⊙O相切于点A.
(2)在图(2)中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗?请说明理由.
(2)在图(2)中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗?请说明理由.

考点:切线的判定
专题:证明题
分析:(1)根据圆周角定理由AB为直径得∠ACB=90°,所以∠B+∠BAC=90°,由于∠CAE=∠B,则∠CAE+∠BAC=90°,所以OA⊥AE,则可根据切线的判定定理得到AE与⊙O相切于点A;
(2)作直径AD,根据圆周角定理得到∠B=∠D,则可与(1)中的证明方法一样得到AE与⊙O相切于点A.
(2)作直径AD,根据圆周角定理得到∠B=∠D,则可与(1)中的证明方法一样得到AE与⊙O相切于点A.
解答:证明:(1)∵AB为直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
而∠CAE=∠B,
∴∠CAE+∠BAC=90°,即∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A;
(2)AE还与⊙O相切于点A.理由如下:
作直径AD,如图2,
∴∠D+∠DAC=90°,
∵∠B=∠D,
而∠CAE=∠B,
∴∠CAE+∠DAC=90°,即∠DAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
∴∠ACB=90°,
∴∠B+∠BAC=90°,
而∠CAE=∠B,
∴∠CAE+∠BAC=90°,即∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A;
(2)AE还与⊙O相切于点A.理由如下:
作直径AD,如图2,
∴∠D+∠DAC=90°,
∵∠B=∠D,
而∠CAE=∠B,
∴∠CAE+∠DAC=90°,即∠DAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知反比例函数y=
的图象经过点(2,-4),则k的值为( )
| k |
| x |
| A、4 | ||
B、-
| ||
| C、-4 | ||
| D、-8 |
 为促进区域经济的快速发展,加快铁路建设,洛堪铁路娄邵段复线工程经过我县甘棠镇.在甘棠镇内铁路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
为促进区域经济的快速发展,加快铁路建设,洛堪铁路娄邵段复线工程经过我县甘棠镇.在甘棠镇内铁路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, 如图,在平面直角坐标系中,直线y=-x+b经过点C(2,4),与x轴,y轴分别相交于点B,A,直线DE与x轴交于点D(18,0),与直线AB相交于点E,点E在第二象限.
如图,在平面直角坐标系中,直线y=-x+b经过点C(2,4),与x轴,y轴分别相交于点B,A,直线DE与x轴交于点D(18,0),与直线AB相交于点E,点E在第二象限.