题目内容
5. 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.(1)若∠D=70°,∠BED=30°,则∠EMA=85(度);
(2)若∠B=60°,∠BCD=40°,则∠ENC=80(度);
(3)∠F与∠B、∠D有怎样的数量关系?证明你的结论.
分析 (1)根据EF为∠BED的平分线可得∠DEF=15°,由∠EMA=∠D+∠DEF,∠D=70°,可以求得∠EMA的度数;
(2)根据CF为∠BCD的平分线可得∠BCN=20°,由∠ENC=∠B+∠BCN,∠B=60°,可以求得∠ENC的度数;
(3)∠F=$\frac{1}{2}$(∠B+∠D),由三角形的外角等于和它不相邻的两个内角的和,三角形的角平分线的知识可以得到∠B,∠D,∠F三者之间的关系,从而证明结论.
解答 解:(1)∵EF为∠BED的平分线,∠BED=30°,
∴∠DEM=∠FEN=$\frac{1}{2}$∠BED=15°.
又∵∠EMA=∠D+∠DEM,∠D=70°,
∴∠EMA=85°.
故答案为:85°.
(2)∵CF为∠BCD的平分线,∠BCD=40°,
∴∠BCN=∠FCM=$\frac{1}{2}$∠BCD=20°.
又∵∠ENC=∠B+∠BCN,∠B=60°,
∴∠ENC=80°.
故答案为:80°.
(3)∠F=$\frac{1}{2}$(∠B+∠D).
证明:∵∠EMA=∠D+∠DEF=∠F+∠DCF,
∠ENC=∠B+∠BCF=∠F+∠BEF,
∴∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF.
又∵CF为∠BCD的平分线,EF为∠BED的平分线,
∴∠DEF=∠BEF,∠DCF=∠BCF.
∴∠B+∠D=2∠F.
即:∠F=$\frac{1}{2}$(∠B+∠D).
点评 本题主要考查三角形角平分线和三角形的外角的知识,关键是明确三角形的外角等于和它不相邻的两个内角的和,进行灵活变化,证明出相应的结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列四组有理数的大小比较正确的是( )
| A. | $-\frac{1}{2}>-\frac{1}{3}$ | B. | -|-1|>-|+1| | C. | $-\frac{4}{5}<-\frac{5}{6}$ | D. | $|{-\frac{1}{2}}|>|{-\frac{1}{3}}|$ |
 已知函数y=-x2-2x+3.
已知函数y=-x2-2x+3.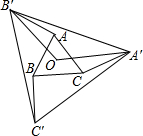 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′. 图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.
图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.