题目内容
已知a+b=2,则a2-b2+4b的值为 .
已知x1,x2为方程x2+4x+2=0的两实根,则x13+14x2+55= .
已知x1,x2为方程x2+4x+2=0的两实根,则x13+14x2+55=
考点:根与系数的关系,完全平方公式,一元二次方程的解
专题:
分析:由a2-b2+4b=(a+b)(a-b)+4b,将a+b=2代入即可求得答案;
由x1,x2为方程x2+4x+2=0的两实根,根据根与系数的关系与方程根的定义,可得x1+x2=-4,x1•x2=2,x12+4x1+2=0,然后将原式变形为x13+14x2+55=x1(-4x1-2)+14x2+55,继而可求得答案.
由x1,x2为方程x2+4x+2=0的两实根,根据根与系数的关系与方程根的定义,可得x1+x2=-4,x1•x2=2,x12+4x1+2=0,然后将原式变形为x13+14x2+55=x1(-4x1-2)+14x2+55,继而可求得答案.
解答:解:∵a+b=2,
∴a2-b2+4b=(a+b)(a-b)+4b=2(a-b)+4b=2a-2b+4b=2a+2b=2(a+b)=2×2=4;
∵x1,x2为方程x2+4x+2=0的两实根,
∴x1+x2=-4,x1•x2=2,x12+4x1+2=0,
∴x12=-4x1-2,
∴x13+14x2+55
=x1(-4x1-2)+14x2+55
=-4x12-2x1+14x2+55
=-4(x12+4x1+2)+14x1+14x2+55+8
=14(x1+x2)+63
=14×(-4)+63
=7.
故答案为:4,7.
∴a2-b2+4b=(a+b)(a-b)+4b=2(a-b)+4b=2a-2b+4b=2a+2b=2(a+b)=2×2=4;
∵x1,x2为方程x2+4x+2=0的两实根,
∴x1+x2=-4,x1•x2=2,x12+4x1+2=0,
∴x12=-4x1-2,
∴x13+14x2+55
=x1(-4x1-2)+14x2+55
=-4x12-2x1+14x2+55
=-4(x12+4x1+2)+14x1+14x2+55+8
=14(x1+x2)+63
=14×(-4)+63
=7.
故答案为:4,7.
点评:此题考查了根与系数的关系、方程的解定义、平方差公式等知识.此题难度适中,解题的关键是将原多项式拆项,利用整体思想求解.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
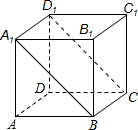 如图在棱长为1的正方体ABCD-A1B1C1D1中,一只蚂蚁从点A出发,沿正方体表面爬行到面对角线A1B上的一点P,再沿截面A1BCD1爬行到点D1,则整个过程中蚂蚁爬行的最短路程为( )
如图在棱长为1的正方体ABCD-A1B1C1D1中,一只蚂蚁从点A出发,沿正方体表面爬行到面对角线A1B上的一点P,再沿截面A1BCD1爬行到点D1,则整个过程中蚂蚁爬行的最短路程为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
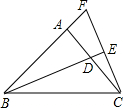 等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△FBC的面积为( )
等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△FBC的面积为( )| A、40 | B、46 | C、48 | D、50 |
化简
等于( )
| (sin28°-cos28°)2 |
| A、sin28°-cos28° |
| B、0 |
| C、cos28°-sin28° |
| D、以上都不对 |
下列等式成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长. 如图,点M、P、N在同一直线上,△AMP、△BPN均为等边三角形,MB、NA相交于Q,则∠AQM=
如图,点M、P、N在同一直线上,△AMP、△BPN均为等边三角形,MB、NA相交于Q,则∠AQM=