题目内容
现将背面完全相同,正面分别标有数-2,-1,0,1,2,3的6张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数记为m,则关于x的一元二次方程mx2+2(m-1)x+m+1=0有实数根的概率为 .
考点:概率公式,根的判别式
专题:
分析:先根据根的判别式求出m的取值范围,再找到符合条件的m值,根据概率公式即可求得关于x的一元二次方程mx2+2(m-1)x+m+1=0有实数根的概率.
解答:解:∵△=[2(m-1)]2-4m(m+1)=-12m+4≥0,
解得m≤
,
∵mx2+2(m-1)x+m+1=0是关于x的一元二次方程,
∴m≠0,
∴正面分别标有数-2,-1,0,1,2,3的6张卡片中符合条件的有-2,-1,共2个.
∴关于x的一元二次方程mx2+2(m-1)x+m+1=0有实数根的概率为2÷6=
.
故答案为
.
解得m≤
| 1 |
| 3 |
∵mx2+2(m-1)x+m+1=0是关于x的一元二次方程,
∴m≠0,
∴正面分别标有数-2,-1,0,1,2,3的6张卡片中符合条件的有-2,-1,共2个.
∴关于x的一元二次方程mx2+2(m-1)x+m+1=0有实数根的概率为2÷6=
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:考查了一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.
同时考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.
同时考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
| m |
| n |

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
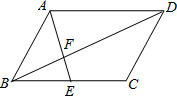 ?ABCD中,E是BC的中点,AE=9,BD=12,AD=10,则△ABD的面积为( )
?ABCD中,E是BC的中点,AE=9,BD=12,AD=10,则△ABD的面积为( )| A、24 | B、30 | C、36 | D、40 |
计算(-2)2+(
)0×5所得的结果是( )
| 3 |
| A、4 | B、9 | C、-l | D、1 |
直线y=kx+k和双曲线y=
在同一坐标系中图象大致正确的是( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
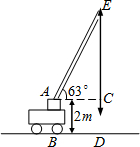 如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)
如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)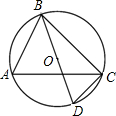 如图,BD是⊙O的直径,∠A=58°,则∠CBD的度数为
如图,BD是⊙O的直径,∠A=58°,则∠CBD的度数为