题目内容
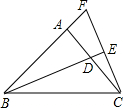 等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△FBC的面积为( )
等腰Rt△ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△FBC的面积为( )| A、40 | B、46 | C、48 | D、50 |
考点:全等三角形的判定与性质,三角形的面积,等腰直角三角形
专题:计算题
分析:求出∠ABD=∠ACF,根据ASA证△ABD≌△ACF,推出AD=AF,得出AB=AC=2AD=2AF,求出AF长,求出AB、AC长,根据三角形的面积公式得出△FBC的面积等于
BF×AC,代入求出即可.
| 1 |
| 2 |
解答:解:∵CE⊥BD,
∴∠BEF=90°,
∵∠BAC=90°,
∴∠CAF=90°,
∴∠FAC=∠BAD=90°,∠ABD+∠F=90°,∠ACF+∠F=90°,
∴∠ABD=∠ACF,
∵在△ABD和△ACF中
,
∴△ABD≌△ACF,
∴AD=AF,
∵AB=AC,D为AC中点,
∴AB=AC=2AD=2AF,
∵BF=AB+AF=12,
∴3AF=12,
∴AF=4,
∴AB=AC=2AF=8,
∴△FBC的面积是
×BF×AC=
×12×8=48,
故选C.
∴∠BEF=90°,
∵∠BAC=90°,
∴∠CAF=90°,
∴∠FAC=∠BAD=90°,∠ABD+∠F=90°,∠ACF+∠F=90°,
∴∠ABD=∠ACF,
∵在△ABD和△ACF中
|
∴△ABD≌△ACF,
∴AD=AF,
∵AB=AC,D为AC中点,
∴AB=AC=2AD=2AF,
∵BF=AB+AF=12,
∴3AF=12,
∴AF=4,
∴AB=AC=2AF=8,
∴△FBC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了三角形的面积,全等三角形的性质和判定,等腰直角三角形的应用,关键是求出AF=AD,主要考查学生运用性质进行计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算(-2)2+(
)0×5所得的结果是( )
| 3 |
| A、4 | B、9 | C、-l | D、1 |
 如图ABCD是正方形,标出的其余各点都是所在边的三等分点.试问图中有多少个矩形(包括正方形)?
如图ABCD是正方形,标出的其余各点都是所在边的三等分点.试问图中有多少个矩形(包括正方形)?
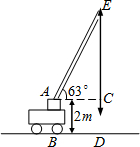 如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)
如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)