题目内容
化简
等于( )
| (sin28°-cos28°)2 |
| A、sin28°-cos28° |
| B、0 |
| C、cos28°-sin28° |
| D、以上都不对 |
考点:同角三角函数的关系
专题:计算题
分析:根据cos28°=sin62°,再有sinx在0°≤x≤90°之间为增函数,可得出sin28°及cos28°的大小关系,继而可得出答案.
解答:解:由题意得,cos28°=sin62°,
又∵sinx在0°≤x≤90°之间为增函数,
∴sin28°<sin62°=cos28°,
故
=cos28°-sin28°.
故选C.
又∵sinx在0°≤x≤90°之间为增函数,
∴sin28°<sin62°=cos28°,
故
| (sin28°-cos28°)2 |
故选C.
点评:此题考查了同角三角函数的知识,解答本题的关键是判断出sin28°与cos28°之间的大小关系,属于基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
计算(-2)2+(
)0×5所得的结果是( )
| 3 |
| A、4 | B、9 | C、-l | D、1 |
方程6xy+4x-9y-7=0的整数解的个数为( )
| A、1 | B、2 | C、3 | D、4 |
在Rt△ABC中,∠C=90°.AB=5,BC=3,则以AC所在直线为轴将Rt△ABC旋转一周得到的几何体的体积是( )
| A、12π | B、16π |
| C、25π | D、20π |
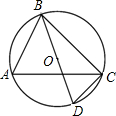 如图,BD是⊙O的直径,∠A=58°,则∠CBD的度数为
如图,BD是⊙O的直径,∠A=58°,则∠CBD的度数为 如图,在平面直角坐标系中,平行四边形ABCO的边OA在x轴上,O(0,0),A(3,0),B(5,1).
如图,在平面直角坐标系中,平行四边形ABCO的边OA在x轴上,O(0,0),A(3,0),B(5,1).