题目内容
14.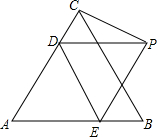 如图,等边三角形ABC的边长为6cm,AD=AE=4cm,连接DE,将△ADE绕点D逆时针旋转,得到△DEP,连接CP,则CP的长是2$\sqrt{3}$cm.
如图,等边三角形ABC的边长为6cm,AD=AE=4cm,连接DE,将△ADE绕点D逆时针旋转,得到△DEP,连接CP,则CP的长是2$\sqrt{3}$cm.
分析 如图,DP交BC于F,由△ABC为等边三角形得到∠BAC=∠ACB=60°,AC=6,再利用AD=AE=4可判断△ADE为等边三角形,CD=2,则根据等边三角形的性质得∠ADE=60°,DE=AD=4,接着根据旋转的性质得∠EDP=60°,DP=DE=4,利用平角的定义可计算出∠PDC=60°,则可判断△DCF为等边三角形,得到∠3=60°,DF=CF=DC=2,所以PF=DP-DF=2,则FC=FP,所以∠1=∠2,然后计算出∠1=30°,于是得到∠PCD=90°,最后在Rt△PCD中利用勾股定理计算PC的长.
解答 解:如图,DP交BC于F,
∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,AC=6,
∵AD=AE=4,
∴△ADE为等边三角形,CD=2,
∴∠ADE=60°,DE=AD=4,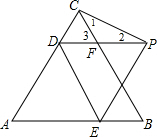
∵△ADE绕点D逆时针旋转60°,得到△DEP,
∴∠EDP=60°,DP=DE=4,
∴∠PDC=60°,
∴△DCF为等边三角形,
∴∠3=60°,DF=CF=DC=2,
∴PF=DP-DF=4-2=2,
∴FC=FP,
∴∠1=∠2,
∵∠3=∠1+∠2,
∴∠1=30°,
∴∠PCD=60°+30°=90°,
在Rt△PCD中,PC=$\sqrt{D{P}^{2}-D{C}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(cm).
故答案为2$\sqrt{3}$.
点评 本题考查了转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知|x|=2,|y|=3,且xy<0,则x+y的值是( )
| A. | 1或-1 | B. | 5或-5 | C. | 5或1 | D. | -5或-1 |
19.若有理数满足$\frac{1}{a}+\frac{1}{b}$=0,则下列说法不正确的是( )
| A. | a与b的差是正数 | B. | a与b的和为0 | C. | a与b的积为负数 | D. | a与b的商为-1 |
 如图,已知AB=AC,∠BAD=∠CAE,AD=AE,求证:BD=EC.
如图,已知AB=AC,∠BAD=∠CAE,AD=AE,求证:BD=EC.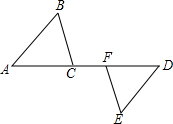 完成推理填空
完成推理填空
 (1)作△ABC的外接圆(尺规作图,保留作图痕迹,不写作法);
(1)作△ABC的外接圆(尺规作图,保留作图痕迹,不写作法);