题目内容
11.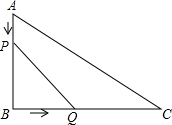 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.(1)设运动开始后第ts时,四边形APQC的面积是Scm2,写出S与t的函数关系式,并指出自变量t的取值范围;
(2)t为何值时,S最小?最小值是多少?
分析 (1)根据t秒时,P、Q两点的运动路程,分别表示PB、BQ的长度,可得△BPQ的面积,用S=S△ABC-S△PBQ求面积即可;
(2)将(1)中所求函数式配方,可得函数的最小值.
解答 解:(1)∵AB=6cm,BC=12cm,∠B=90°,
∴BP=6-t,BQ=2t,
∴S四边形APQC=S△ABC-S△PBQ=$\frac{1}{2}×6×12$-$\frac{1}{2}×(6-t)•2t$,
即:S=t2-6t+36;
(2)∵S=t2-6t+36;
∴S=(t-3)2+27,
∴当t=3时,S最小,最小值是27.
点评 本题考查了二次函数的最值在解决面积问题中的运用.关键是根据所设字母,表示相关线段的长度,再计算面积,把所得的代数式看作二次函数求最值.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
1.19922-1991×1993的计算结果为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
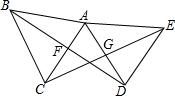 如图,已知AB=AD,AC=AE,∠BAD=∠CAE,DB交AC于点F,且AF平分BD,CE交AD于G,求证:CG=GE.
如图,已知AB=AD,AC=AE,∠BAD=∠CAE,DB交AC于点F,且AF平分BD,CE交AD于G,求证:CG=GE.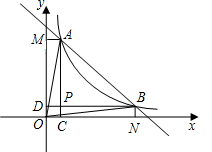 已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )
已知反比例函数y=$\frac{k}{x}$(k>0)的图象与直线y=-x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个( )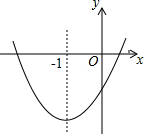 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论: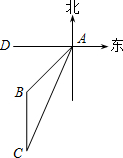 一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距36$\sqrt{2}$海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向.(参考数据:sin24°≈0.4,cos24°≈0.9).
一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距36$\sqrt{2}$海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向.(参考数据:sin24°≈0.4,cos24°≈0.9).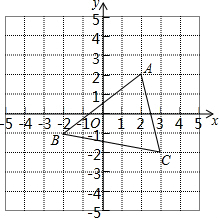 如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.
如图,将△ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度,得到△EFG.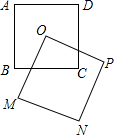 如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.
如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,这两个正方形重叠部分的面积为25.