题目内容
10．
如图，E是△ABC中AB边延长线上一点，∠EBC的平分线交AC延长线于点D，若∠A=40°，∠CBD=68°，求∠D的度数．
分析 根据角平分线定义求出∠CBE，易得∠ABC，根据三角形外角性质求出∠BCD，根据三角形内角和定理求出结果．
解答 解：∵BD为∠CBE的角平分线，∠CBD=68°，
∴∠CBE=136°，
∴∠ABC=180°-136°=44°，
∵∠A=40°，
∴∠BCD=84°，
∴∠D=180°-∠CBD-∠BCD=180°-68°-84°=28°．
点评 本题主要考查了三角形内角和定理，角平分线定义，三角形外角性质，注意：三角形的内角和等于180°，三角形的一个外角等于和它不相邻的两个内角之和是解答此题的关键．
练习册系列答案
相关题目
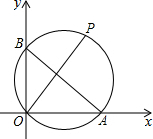如图，已知A、B两点的坐标分别为（4，0）、（0，3），P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为（$\frac{7}{2}$，$\frac{7}{2}$）或（$\frac{1}{2}$，-$\frac{1}{2}$）．
1．19922-1991×1993的计算结果为（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
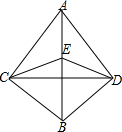已知：如图，AC=AD，BC=BD，点E在AB上，求证：EC=ED．
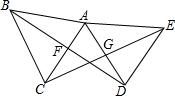如图，已知AB=AD，AC=AE，∠BAD=∠CAE，DB交AC于点F，且AF平分BD，CE交AD于G，求证：CG=GE．
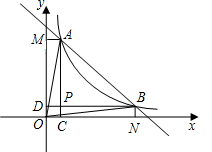已知反比例函数y=$\frac{k}{x}$（k＞0）的图象与直线y=-x+6相交于第一象限A、B的两点．如图所示，过A、B两点分别作x、y轴的垂线，线段AC、BD相交与P，给出以下结论：①OA=OB；②四边形OCPD是正方形；③若k=5．则△ABP的面积是8；④P点一定在直线y=x上，其中正确命题的个数是几个（ ）
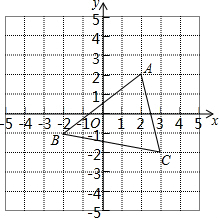如图，将△ABC沿x轴正方向平移2个单位长度，再沿y轴负方向平移1个单位长度，得到△EFG．