题目内容
18. 平面直角坐标系中有直线y=kx-k+4(k≠0),
平面直角坐标系中有直线y=kx-k+4(k≠0),(1)当k取不同的值时函数图象均不同,画出当k分别等于-$\frac{4}{3}$和2时的函数图象l1和l2.(画在同一直角坐标系中)
(2)根据图象,写出你发现的一条结论.
(3)若点A为l1与l2的交点,l1交x轴于点B,点C在y轴上,△ABC是等腰三角形,请确定点C的坐标.
分析 (1)把k=-$\frac{4}{3}$和k=2代入直线y=kx-k+4,化简即可;
(2)图象如图所示,图象恒过点A(1,4),
(3)先确定出点A,B的坐标,设出点C的坐标,表示出AC,BC,AB,再分三种情况建立方程求解即可.
解答 解:(1)当k=-$\frac{4}{3}$时,l1:y=(-$\frac{4}{3}$)x+$\frac{4}{3}$+4=-$\frac{4}{3}$x+$\frac{16}{3}$,
当k=2时,l2:y=2x-2+4=2x+2,
(2)图象如图所示,
结论:图象是一条直线,图象过定点(1,4),
(3)由(1)有,l1:y=-$\frac{4}{3}$x+$\frac{16}{3}$,l2:y=2x+2
∵点A为l1与l2的交点,
∴A(1,4),
∵l1交x轴于点B,
∴令y=0,-$\frac{4}{3}$x+$\frac{16}{3}$=0,
∴x=4,
∴B(4,0),
∴AB2=25,
设点C(0,a),
∴AC2=(a-4)2+1,BC2=a2+16,
∵△ABC是等腰三角形
①当AB=AC时,
∴AB2=AC2,
∴(a-4)2+1=25,
∴a=4±2$\sqrt{6}$,
∴C1(0,4+2$\sqrt{6}$),C2(0,4-2$\sqrt{6}$),
②当BA=BC时,
∴AB2=BC2,
∴a2+16=25,
∴a=±3,
∴C3(0,3),C4(0,-3)
③当CA=CB时,
∴AC2=BC2,
∴(a-4)2+1=a2+16,
∴a=$\frac{1}{8}$,
∴C5(0,$\frac{1}{8}$).
点评 此题是一次函数综合题,主要考查了函数图象的画法,直线交点坐标的求法,等腰三角形的性质,分类思想是解本题的关键.

练习册系列答案
相关题目
13. 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )| A. | 段① | B. | 段② | C. | 段③ | D. | 段④ |
7. 如图,AB是⊙O的直径,C、D是⊙O上两点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则cos∠E等于( )
如图,AB是⊙O的直径,C、D是⊙O上两点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则cos∠E等于( )
 如图,AB是⊙O的直径,C、D是⊙O上两点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则cos∠E等于( )
如图,AB是⊙O的直径,C、D是⊙O上两点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则cos∠E等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
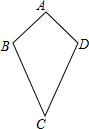 有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形,请探究筝形的性质和判定方法.
有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形,请探究筝形的性质和判定方法.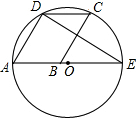 如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.
如图,已知平行四边形ABCD的顶点A、D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=58°.