题目内容
3.如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90°,BE=EF,连接DF,点P是FD的中点,连接PE、PC.(1)如图1,当点E在CB边上时,求证:PE=$\frac{{\sqrt{2}}}{2}$CE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明.

分析 (1)延长EP交DC于点G,由正方形的性质和已知条件可证明△PEF≌△PGD(AAS),进而可证明△CGE是等腰直角三角形,则CP⊥GE,CP=$\frac{1}{2}$EG=PE,所以△CPE是等腰直角三角形.由等腰三角形的性质可得PE=$\frac{\sqrt{2}}{2}$CE,问题得证;
(2)PE=$\frac{\sqrt{2}}{2}$CE,延长EP交CD的延长线于点G,由(1)的证明思路即可证得.
解答 解:(1)延长EP交DC于点G,如图(1)所示:
∵∠FEC=∠DCE=90°,
∴EF∥CD,
∴∠PFE=∠PDG,
又∵∠EPF=∠GPD,PF=PD,
∴在△PEF和△PGD中
$\left\{\begin{array}{l}{∠PFE=∠PDG}\\{∠EPF=∠GPD}\\{PF=PD}\end{array}\right.$
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=$\frac{1}{2}$EG=PE,
∴△CPE是等腰直角三角形.
∴PE=$\frac{\sqrt{2}}{2}$CE;
(2)PE=$\frac{\sqrt{2}}{2}$CE,理由如下:如图(2)所示:
延长EP交CD的延长线于点G,
∵∠FEB+∠DCB=180°,
∴EF∥CD,
∴∠PEF=∠PGD,
又∵∠EPF=∠GPD,PF=PD,
∴在△PEF和△PGD中,
$\left\{\begin{array}{l}{∠PFE=∠PDG}\\{∠EPF=∠GPD}\\{PF=PD}\end{array}\right.$,
∴△PEF≌△PGD(AAS),
∴PE=PG,EF=GD,
∵BE=EF,
∴BE=GD.
∵CD=CB,
∴CG=CE,
∴△CGE是等腰直角三角形,
∴CP⊥GE,CP=$\frac{1}{2}$EG=PE,
∴△CPE是等腰直角三角形.
∴PE=$\frac{\sqrt{2}}{2}$CE.
点评 本题考查了四边形的综合性题目,用到的知识点有正方形的性质、全等三角形的判定和性质、等腰三角形三角形的判定和性质,题目的综合性较强,难度较大,熟记各种特殊几何图形的判定方法和性质是解题的关键.

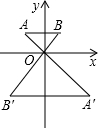 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )| A. | (-x,-y) | B. | (-2x,-2y) | C. | (-2x,2y) | D. | (2x,-2y) |
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.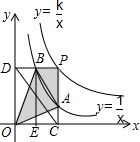 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论:
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$的图象上运动时,以下结论: 平面直角坐标系中有直线y=kx-k+4(k≠0),
平面直角坐标系中有直线y=kx-k+4(k≠0), 如图,将正方体相邻的两个面上分别画出3×3的正方形网格,并分别用图形“
如图,将正方体相邻的两个面上分别画出3×3的正方形网格,并分别用图形“ ”和“○”在网格内的交点处做上标记,则该正方体的表面展开图是( )
”和“○”在网格内的交点处做上标记,则该正方体的表面展开图是( )







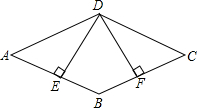 如图,已知四边形ABCD是菱形,DE⊥AB于E,DF⊥BC于F.求证:△ADE≌△CDF.
如图,已知四边形ABCD是菱形,DE⊥AB于E,DF⊥BC于F.求证:△ADE≌△CDF.