题目内容
13.在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与直线CF相交于点G.(1)若点D在线段BC上,如图(1),判断:线段BC与线段CG的数量关系:BC=CG,位置关系:BC⊥CG.
(2)如图(2),①若点D在线段BC的延长线上,(1)中判断线段BC与线段CG的数量关系与位置关系是否仍然成立,并说明理由;
②当G为CF中点,连接GE,若AB=$\sqrt{2}$,求线段GE的长.

分析 (1)根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;
(2)①根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;②与①同理,可得BD=CF,BC=CG,BC⊥CG,根据已知条件得到BC=CG=FG=CD=2,如图(2),过点A作AM⊥BD于M,根据勾股定理得到AD=$\sqrt{10}$,过点E作EN⊥FG于N,根据全等三角形的性质得到FG=AM=1,推出NE为FG的垂直平分线,即可得到结论.
解答 解:(1)BC=CG,BC⊥CG,
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
则在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠B=45°,BD=CF,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CG,
同理△ADC≌△AFG,
∴CD=GF,
∴BD+CD=CF+GF,
即BC=CG,
故答案为:BC=CG,BC⊥CG;
(2)①仍然成立
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
则在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠B=45°,BD=CF,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CG,
同理△ADC≌△AFG,
∴CD=GF,
∴BD+CD=CF+GF,
即BC=CG, ②与①同理,可得BD=CF,BC=CG,BC⊥CG,
②与①同理,可得BD=CF,BC=CG,BC⊥CG,
∵AB=$\sqrt{2}$,G为CF中点,
∴BC=CG=FG=CD=2,
如图(2),过点A作AM⊥BD于M,
∴AM=1,MD=3,
∴AD=$\sqrt{10}$,
过点E作EN⊥FG于N,
在△AMD与△FNE中,$\left\{\begin{array}{l}{∠FEN=∠ADM}\\{∠ENF=∠AMD=90°}\\{EF=AD}\end{array}\right.$,
∴△AMD≌△FNE,
∴FN=AM=1,
∴FG=2FN,
∴NE为FG的垂直平分线,
即CE=FE=AD=$\sqrt{10}$.
点评 本题考查了全等三角形的判定和性质,正方形的性质,等腰直角三角形的性质,熟练掌握全等三角形的判定和性质解题的关键.

| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S甲2<S乙2 | B. | $\overline{x}$甲=$\overline{x}$乙,S甲2>S乙2 | ||
| C. | $\overline{x}$甲>$\overline{x}$乙,S甲2<S乙2 | D. | $\overline{x}$甲>$\overline{x}$乙,S甲2>S乙2 |
| A. | 要了解人们对“低碳生活”的了解程度,宜采用普查方式 | |
| B. | 一组数据5,5,6,7的众数和中位数都是5 | |
| C. | 必然事件发生的概率为100% | |
| D. | 若甲组数据的方差是3.4,乙组数据的方差是1.68,则甲组数据比乙组数据稳定 |
| A. | 6π | B. | 4π | C. | 2π | D. | π |
 如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )
如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
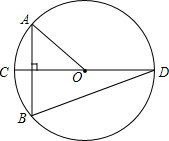 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
| A. |  | B. |  | C. |  | D. |  |
 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.