题目内容
15. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )| A. | 10 | B. | 8$\sqrt{2}$ | C. | 4$\sqrt{13}$ | D. | 2$\sqrt{41}$ |
分析 如图连接BM、OM,AM,作MH⊥BC于H,先证明四边形OAMH是矩形,根据垂径定理求出HB,在RT△AOM中求出OM即可.
解答 解:如图连接BM、OM,AM,作MH⊥BC于H.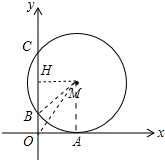
∵⊙M与x轴相切于点A(8,0),
∴AM⊥OA,OA=8,
∴∠OAM=∠MH0=∠HOA=90°,
∴四边形OAMH是矩形,
∴AM=OH,
∵MH⊥BC,
∴HC=HB=6,
∴OH=AM=10,
在RT△AOM中,OM=$\sqrt{A{M}^{2}+O{A}^{2}}$=$\sqrt{{8}^{2}+1{0}^{2}}$=2$\sqrt{41}$.
故选D.
点评 本题考查切线的性质、坐标与图形性质、垂径定理、勾股定理等知识,解题的关键是正确添加辅助线,构造直角三角形.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列二次根式,是同类二次根式的是( )
| A. | $\sqrt{2}与\sqrt{3}$ | B. | $\sqrt{12}与\sqrt{27}$ | C. | $\sqrt{a}与\sqrt{b}$ | D. | $\sqrt{a}与\sqrt{2a}$ |
7.某品牌运动鞋销售商在进行市场占有率的调查时,他最关注的是( )
| A. | 运动鞋型号的平均数 | B. | 运动鞋型号的众数 | ||
| C. | 运动鞋型号的中位数 | D. | 运动鞋型号的极差 |
4.不等式组$\left\{\begin{array}{l}{2x-1≤3}\\{x+3>4}\end{array}\right.$的解集是( )
| A. | x>1 | B. | 1<x≤2 | C. | x≤2 | D. | 无解 |
5.已知a2+3a=1,则代数式2a2+6a-1的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25. 如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.