题目内容
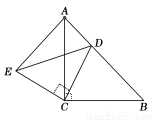
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
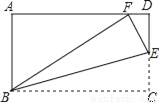
【答案】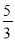
【解析】试题分析:由矩形的性质可得AB=CD=4,AD=BC=5,再根据折叠的性质可得CE=EF,BF=BC=5.在Rt△ABF中,根据勾股定理可求得AF=4,设CE=x,在Rt△EDF中,由勾股定理可得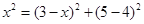 ,解得x=
,解得x=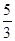 ,即CE的长为
,即CE的长为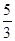 .
.
考点:矩形的性质;折叠的性质;勾股定理.
【题型】填空题
【结束】
14
观察下列各式: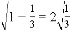 ,
,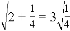 ,
,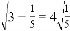 …请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。
…请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目


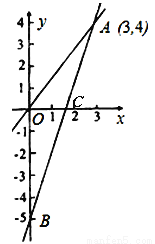
 ,预计2014年将达到4840元/
,预计2014年将达到4840元/
 (4,4);(3)作图如下:
(4,4);(3)作图如下: (0,-3).
(0,-3).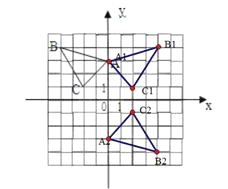
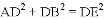 .
.
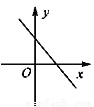 B.
B. 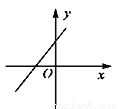 C.
C. 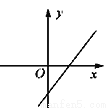 D.
D. 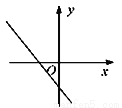
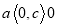 ,故选A.
,故选A.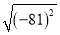 的算术平方根是____.
的算术平方根是____.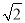 ,3 B.
,3 B. 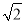 ,
, 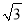 ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. 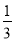 ,
, 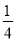 ,
, 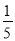
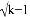 x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0根的情况为( )
x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0根的情况为( )