题目内容
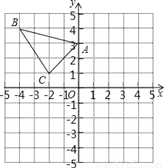
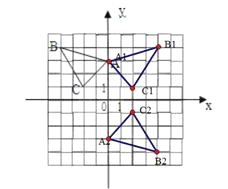
△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
【答案】(1)A(0,3);B(﹣4,4);C(﹣2,1);(2)B1的坐标为:(4,4);(3)A2(0,﹣3)
【解析】试题分析:(1)根据三角形在平面直角坐标系的位置,分别写出作标点;(2)作关于y轴对称的图形见解析;(3)作关于原点对称图形见解析;
试题解析:(1)根据平面直角坐标系可知点A,B,C的坐标为A(0,3);B(-4,4);C(-2,1);
(2)作图如下图: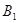 (4,4);(3)作图如下:
(4,4);(3)作图如下: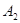 (0,-3).
(0,-3).
考点:1.作图-轴对称变换2.作图-中心对称变换3.象限内点的坐标
【题型】解答题
【结束】
19
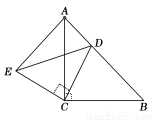
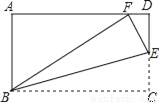
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
(1)△ACE≌△BCD;(2)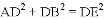 .
.
练习册系列答案
相关题目


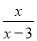 有意义的x的取值范围是( )
有意义的x的取值范围是( )
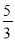
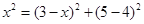 ,解得x=
,解得x=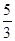 ,即CE的长为
,即CE的长为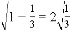 ,
,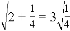 ,
,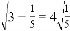 …请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。
…请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。