题目内容
5.下列各式中计算正确的是( )| A. | $\sqrt{(-1)(-9)}$=$\sqrt{-1}$•$\sqrt{-9}$=(-1)(-3)=3 | B. | $\sqrt{(-2)^{2}}$=-2 | ||
| C. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | D. | $\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7 |
分析 根据$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$(a≥0,b≥0),进行化简,再选择即可.
解答 解:A、$\sqrt{(-1)(-9)}$=$\sqrt{1}$•$\sqrt{9}$=1×3=3,故A错误;
B、$\sqrt{(-2)^{2}}$=2,故B错误;
C、$\sqrt{{3}^{2}+{4}^{2}}$=$\sqrt{25}$=5,故C错误;
D、$\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7,故D正确;
故选D.
点评 本题考查了二次根式的化简求值,以及二次根式的乘除法运算,掌握$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$(a≥0,b≥0)是解题的关键.

练习册系列答案
相关题目
15.(-2)2014+3×(-2)2013的值为( )
| A. | -22013 | B. | 22013 | C. | 22014 | D. | 22014 |
13.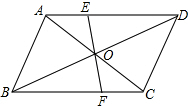 如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
 如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )| A. | 3对 | B. | 4对 | C. | 6对 | D. | 8对 |
14.已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是( )
| A. | AC=BD AB∥CD,AB=CD | B. | AD∥BC,∠A=∠C | ||
| C. | AO=BO=CO=DO,AC⊥BD | D. | AO=CO,BO=DO,AB=BC |