题目内容
16.计算:(1)$\sqrt{16}$-$\root{3}{125}$+|$\sqrt{3}$-2|
(2)$\sqrt{36}$-$\root{3}{27}$+$\sqrt{\frac{9}{4}}$×$\root{3}{-8}$
(3)化简:(2$\sqrt{3}$+3$\sqrt{2}$)-|-$\sqrt{2}$|
分析 (1)原式利用平方根,立方根的定义,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方根及立方根定义计算即可得到结果;
(3)原式利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)原式=4-5+2-$\sqrt{3}$=1-$\sqrt{3}$;
(2)原式=6-3+$\frac{3}{2}$×(-2)=6-3-3=0;
(3)原式=2$\sqrt{3}$+3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{3}$+2$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
7.已知-2<m<3,化简$\sqrt{(m-3)^{2}}$+|m+2|的结果是( )
| A. | 5 | B. | 1 | C. | 2m-1 | D. | 2m-5 |
8.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 5,12,14 | B. | 6,8,10 | C. | 7,24,25 | D. | 8,15,17 |
5.下列各式中计算正确的是( )
| A. | $\sqrt{(-1)(-9)}$=$\sqrt{-1}$•$\sqrt{-9}$=(-1)(-3)=3 | B. | $\sqrt{(-2)^{2}}$=-2 | ||
| C. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | D. | $\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7 |
6. 已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
 已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论中正确的是( )| A. | a<b | B. | ab<0 | C. | b-a>0 | D. | a+b<0 |
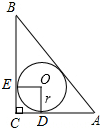 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.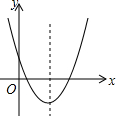 二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.
二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.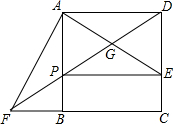 如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.
如图,在正方形ABCD中,点E时CD边上一点,AF⊥AE交CB的延长线于点F,连接DF分别交于AE、AB于点C、P连接PE.