题目内容
13.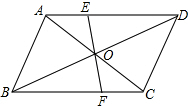 如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )| A. | 3对 | B. | 4对 | C. | 6对 | D. | 8对 |
分析 根据已知及全等三角形的判定方法进行分析,从而得到答案.
解答 解:∵四边形ABCD为平行四边形,其平行四边形的对角线相互平分,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∵∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△AOE≌△COF(ASA),△DOE≌△BOF(ASA),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共有6对.
故选C.
点评 此题主要考查全等三角形的判定方法,常用的判定方法有AAS,SAS,SSS,ASA等.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.

练习册系列答案
相关题目
3. 如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
 如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
8.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 5,12,14 | B. | 6,8,10 | C. | 7,24,25 | D. | 8,15,17 |
5.下列各式中计算正确的是( )
| A. | $\sqrt{(-1)(-9)}$=$\sqrt{-1}$•$\sqrt{-9}$=(-1)(-3)=3 | B. | $\sqrt{(-2)^{2}}$=-2 | ||
| C. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | D. | $\sqrt{2{5}^{2}-2{4}^{2}}$=$\sqrt{25+24}$•$\sqrt{25-24}$=7×1=7 |
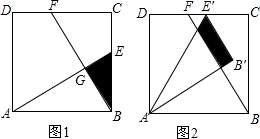
2. 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )| A. | 30° | B. | 45° | C. | 120° | D. | 90° |
3.若实数x,y满足|x-2|+$\sqrt{y+5}$=0,则xy的值是( )
| A. | 10 | B. | 3 | C. | 7 | D. | -10 |
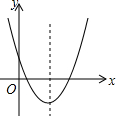 二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.
二次函数的图象如图所示,其对称轴为x=$\frac{3}{2}$,A(2,y1),B($\frac{4}{3}$,y2)两点均在二次函数的图象上,则y1与y2的大小关系为y1>y2.