题目内容
18.在?ABCD中,点E在射线CA上,CE=2AE,射线BE交直线AD于点F,BF=3,则BE的长为2.分析 根据平行四边形的性质可得AF∥BC,从而可证明△AEF∽△CEB,根据相似三角形的性质可得$\frac{AE}{CE}$=$\frac{EF}{BE}$=$\frac{1}{2}$,再由条件BF=3可得BE的长.
解答  解:解:∵四边形ABCD是平行四边形,
解:解:∵四边形ABCD是平行四边形,
∴AF∥BC,
∴△AEF∽△CEB,
∴$\frac{AE}{CE}$=$\frac{EF}{BE}$,
∵CE=2AE,
∴$\frac{EF}{BE}$=$\frac{1}{2}$,
∵BF=3,
∴BE=2,
故答案为2.
点评 此题主要考查了平行四边形的性质,以及相似三角形的判定和性质,关键是掌握平行四边形对边平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列条件中,能判定△ABC≌△DEF的是( )
| A. | ∠A=∠D,∠C=∠F,∠B=∠E | B. | ∠B=∠E,AB=ED,AC=DF | ||
| C. | ∠A=∠D,∠B=∠E,AC=DF | D. | ∠A=∠D,AB=DE,BC=EF |
13.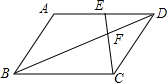 如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
 如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )| A. | CF=2EF | B. | BC=2AE | C. | CE=2EF | D. | AE=ED |
7. 如图,△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC,垂足为点E,若∠BAD=15°,则∠CBE的度数为( )
如图,△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC,垂足为点E,若∠BAD=15°,则∠CBE的度数为( )
 如图,△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC,垂足为点E,若∠BAD=15°,则∠CBE的度数为( )
如图,△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC,垂足为点E,若∠BAD=15°,则∠CBE的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
8. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,在平行四边形EFGH中,它的周长为30,EF=6,则EH=9.
如图,在平行四边形EFGH中,它的周长为30,EF=6,则EH=9.