题目内容
12. 如图,平面上六个点A,B,C,D,E,F构成一个封闭的折线图形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,平面上六个点A,B,C,D,E,F构成一个封闭的折线图形.求证:∠A+∠B+∠C+∠D+∠E+∠F=360°.
分析 连接DE,如图,根据三角形外角的性质可得∠A+∠B=∠PED+∠PDE,从而把等式左边的角度和转化为四边形CDEF的内角和,问题得以解决.
解答  证明:连接DE,如图.
证明:连接DE,如图.
∵∠APE=∠A+∠B,∠APE=∠PED+∠PDE,
∴∠A+∠B=∠PED+∠PDE,
∴∠A+∠B+∠C+∠CDR+∠FEQ+∠F
=∠PED+∠PDE+∠C+∠CDR+∠FEQ+∠F
=∠C+∠CDE+∠DEF+∠F
=360°.
点评 本题主要考查了三角形外角的性质、四边形的内角和定理等知识,把∠A+∠B转化为∠PED+∠PDE,是解决本题的关键.

练习册系列答案
相关题目
15.一列单项式按以下规律排列:x,3x2,5x2,7x,9x2,l1x2,13x,…,则第2015个单项式应是( )
| A. | 4029x | B. | 4029x2 | C. | 4027x | D. | 4027x2 |
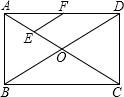 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm. 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数. 如图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的中点,三角形ABC的BC边上的高是4厘米,阴影面积是多少平方厘米?
如图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的中点,三角形ABC的BC边上的高是4厘米,阴影面积是多少平方厘米?