题目内容
2．
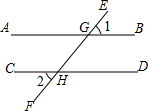（1）先化简再求值：（2x-1）2+（x+2）（x-2）-4x（x-1），其中x=2．（2）已知：如图，AB∥CD，直线EF分别与AB，CD交于点G和点H，∠1=70°，求∠2的度数．
分析 （1）直接利用乘法公式化简原式进而合并同类项，再将已知x=2代入求出答案；
（2）直接利用平行线的性质得出∠GHD的度数，再利用对顶角的性质得出答案．
解答 解：（1）（2x-1）2+（x+2）（x-2）-4x（x-1），
=4x2-4x+1+x2-4-4x2+4x
=x2-3
把x=2代入上式可得：原式=22-3=1；
（2）∵AB∥CD，∠1=70°，
∴∠GHD=∠1=70°，
∴∠2=70°．
点评 此题主要考查了整式的混合运算以及平行线的性质，正确掌握乘法公式是解题关键．
练习册系列答案
相关题目
17．
尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于$\frac{1}{2}$CD长为半径画弧，两弧交于点P，作射线OP，由作法可得△OCP≌△ODP，判定这两个三角形全等的根据是（ ）
尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于$\frac{1}{2}$CD长为半径画弧，两弧交于点P，作射线OP，由作法可得△OCP≌△ODP，判定这两个三角形全等的根据是（ ）| A． | SAS | B． | ASA | C． | AAS | D． | SSS |
直线l1∥l2，一块含45°角的直角三角板如图放置，∠1=89°，则∠2=44°．
14．化简分式$\frac{m}{m-1}$+$\frac{1}{1-m}$的结果为（ ）
| A． | -1 | B． | 1 | C． | $\frac{m+1}{m-1}$ | D． | $\frac{m+1}{1-m}$ |
如图，将两根钢条AB、CD的中点O连在一起，使AB、CD可以绕点O自由转动，就做成一个测量工件，则AC的长等于内槽宽BD，则判定△OBD≌△OAC的理由是（ ）
看图填空：