题目内容
5.已知x轴上有点A(-1,0),B(3,0)两点,y=x2+2kx+k2-3的图象与线段AB有交点时,k的取值范围是3+$\sqrt{3}$≤k$≤1+\sqrt{3}$或-3-$\sqrt{3}$≤k≤1-$\sqrt{3}$.分析 令y=0得出抛物线与x轴的交点坐标,列出不等式即可解决问题.
解答 解:令y=0,得x2+2kx+k2-3=0,
解得x=-k±$\sqrt{3}$,
∵二次函数y=x2+2ax+3的图象与线段AB有交点,
抛物线与x轴交于(-k+$\sqrt{3}$,0),(-k-$\sqrt{3}$,0),开口向上,
∴当-1≤-k+$\sqrt{3}$≤3时,抛物线与线段AB有交点,即-3+$\sqrt{3}$≤k$≤1+\sqrt{3}$;
或当-1≤-k-≤3时,抛物线与线段AB有交点,即-3-$\sqrt{3}$≤k≤1-$\sqrt{3}$;
故答案为3+$\sqrt{3}$≤k$≤1+\sqrt{3}$或-3-$\sqrt{3}$≤k≤1-$\sqrt{3}$.
点评 本题考查二次函数图象上的点的坐标特征,解题的关键是学会利用图象解决问题,把问题转化为不等式,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.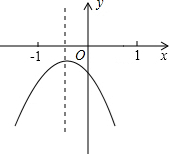 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中,①2a-b<0②abc<0③a+b+c<0④a-b+c<0⑤4a+2b+c>0⑤b2>-4ac错误的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知a、b为实数,则a2+ab+b2-a-2b的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 如图,∠ACB=∠CDB=90°,图中∠ACD的余角有2个.
如图,∠ACB=∠CDB=90°,图中∠ACD的余角有2个. 如图,在?ABCD中,BD是对角线,点M是BC的中点.若AD=10,BD=12,AM=9.则?ABCD面积是72.
如图,在?ABCD中,BD是对角线,点M是BC的中点.若AD=10,BD=12,AM=9.则?ABCD面积是72.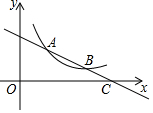 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)