题目内容
18．若关于x的不等式组$\left\{\begin{array}{l}{2a-x＞3}\\{2x+8＞4a}\end{array}\right.$的解集中每一x值均不在-1≤x≤4的范围中，则a的取值范围是a≥4或a≤-2．分析 根据解不等式，可得不等式组的解集，根据不等式组的解集，可得答案．
解答 解：由$\left\{\begin{array}{l}{2a-x＞3}\\{2x+8＞4a}\end{array}\right.$解得
2a-4＜x＜2a+3．
由关于x的不等式组$\left\{\begin{array}{l}{2a-x＞3}\\{2x+8＞4a}\end{array}\right.$的解集中每一x值均不在-1≤x≤4的范围中，得
2a-4≥4或2a+3≤-1．
解得a≥4或a≤-2，
故答案为：a≥4或a≤-2．
点评 本题考查了不等式的解集，利用不等式的解集不在-1≤x≤4的范围中得出2a-4≥4或2a+3≤-1是解题关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图，在⊙O中，AB=AC，∠B=70°，则∠C=70°．
10．
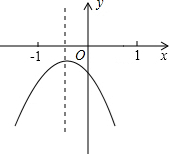已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中，①2a-b＜0②abc＜0③a+b+c＜0④a-b+c＜0⑤4a+2b+c＞0⑤b2＞-4ac错误的个数有（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中，①2a-b＜0②abc＜0③a+b+c＜0④a-b+c＜0⑤4a+2b+c＞0⑤b2＞-4ac错误的个数有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |