题目内容
4. 直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )
直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
分析 根据直线AB与⊙O相切于点A,得出OA⊥AB,再通过特殊角计算出OB的长,最后根据勾股定理求出⊙O的半径.
解答 解:∵直线AB与⊙O相切于点A,
∴OA⊥AB,
∵∠OBA=60°,
∴∠BOA=30°,
∵AB=1,
∴OB=2,
∴OA=$\sqrt{O{B}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴⊙O的半径为$\sqrt{3}$.
故选B.
点评 此题考查了圆的切线的性质:用到的知识点是圆的切线垂直于过切点的半径、含30°的直角三角形的性质:30°所对的边是斜边的一半、勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列运算中结果正确的是( )
| A. | 3a+2b=5ab | B. | 3x2y-2x2y=x2y | C. | -3x+5x=-8x | D. | 5y-3y=2 |
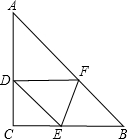 如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.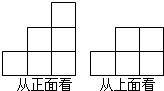 由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )