题目内容
4. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,下面四个结论:①DA平分∠EDF;②EB=FC;③AD上的点到B、C两点的距离相等;④到AE、AF距离相等的点,到DE、DF的距离也相等,其中正确的结论有①②③④.(填序号)
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,下面四个结论:①DA平分∠EDF;②EB=FC;③AD上的点到B、C两点的距离相等;④到AE、AF距离相等的点,到DE、DF的距离也相等,其中正确的结论有①②③④.(填序号)
分析 根据角平分线性质和垂直得出DE=DF,∠AED=∠AFD=90°,∠BED=∠CFD=90°,证Rt△AED≌Rt△AFD,根据全等得出AE=AF,∠EDA=∠FDA,根据角平分线的性质求出AD上的点到B、C两点的距离相等,AD上的点到AE、AF距离相等,即可得出答案.
解答 解:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,∠BED=∠CFD=90°,
在Rt△AED和Rt△AFD中,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,∠EDA=∠FDA,∴①正确;
∵AB=AC,AE=AF,
∴BE=CF,∴②正确;
∵在△ABC中,AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴AD上的点到B、C两点的距离相等,∴③正确;
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴AD上的点到AE、AF距离相等,
∵∠EDA=∠FDA,DE⊥AB,DF⊥AC,
∴AD上的点到DE、DF距离相等,∴④正确;
故答案为:①②③④.
点评 本题考查了等腰三角形的性质,全等三角形的性质和判定,角平分线性质的应用,能正确运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则下列说法中正确的是( )
如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则下列说法中正确的是( )
 如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则下列说法中正确的是( )
如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则下列说法中正确的是( )| A. | a=-2014 | B. | b=-2013 | C. | c=-2015 | D. | 无法确定 |
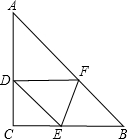 如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.