题目内容
2. 如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )
如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
分析 先由CE=2,DE=8计算出OB=OC=5,OE=3,根据垂径定理的推论,由直径CD过弦AB的中点E得到CD⊥AB,AE=BE,再根据勾股定理计算出BE=4,从而得到AB=8.
解答 解:∵CE=2,DE=8,
∴CD=10,
∴OB=OC=5,OE=5-2=3,
∵直径CD过弦AB的中点E,
∴CD⊥AB,
∴AE=BE,
在Rt△OBE中,∵OE=3,OB=5,
∴BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=4,
∴AB=2BE=8.
故选B.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
11.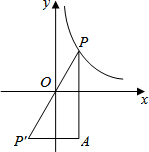 设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
 设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )| A. | 随P点的变化而变化 | B. | 等于1 | ||
| C. | 等于2 | D. | 等于4 |
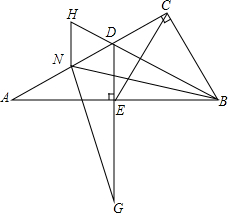 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,连接EC,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,延长BD至H,使DH=DN,连接NH.求证:
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,连接EC,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,延长BD至H,使DH=DN,连接NH.求证: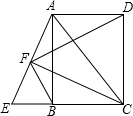 如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点,
如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点, 如图,⊙O的半径是4,P是⊙O内一点,且OP=3,过P点的弦AB与点O形成的△OAB的最大面积为4.
如图,⊙O的半径是4,P是⊙O内一点,且OP=3,过P点的弦AB与点O形成的△OAB的最大面积为4.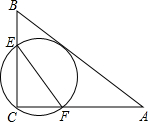 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.