题目内容
7.阅读下列简化过程$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-1}$=$\sqrt{2}$-1
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$
$\frac{1}{\sqrt{4}-\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}$-$\sqrt{3}$
…
从中找出化简的方法规律,然后解答下列问题
(1)计算:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$
(2)设a=$\frac{1}{\sqrt{3}-\sqrt{2}}$,b=$\frac{1}{2-\sqrt{3}}$,c=$\frac{1}{\sqrt{5}-2}$,比较a,b,c的大小关系.
分析 (1)根据分母有理化,可得答案;
(2)根据分母有理化,实数的大小比较,可得答案.
解答 解:(1)原式=($\sqrt{2}$-1)+($\sqrt{3}-\sqrt{2}$)+($\sqrt{4}-\sqrt{3}$)+…+$\sqrt{2016}$-$\sqrt{2015}$
=$\sqrt{2016}$-1
=12$\sqrt{14}$-1;
(2)a=$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$,
b=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
c=$\frac{1}{\sqrt{5}-2}$=$\sqrt{5}$+2,
由$\sqrt{2}$<$\sqrt{3}$<$\sqrt{5}$,得
a<b<c.
点评 本题考查了分母有理化,利用使它们的积符合平方差公式是解答问题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
17.计算:$\sqrt{8}$-$\sqrt{2}$,正确的是( )
| A. | 4 | B. | $\sqrt{6}$ | C. | 2 | D. | $\sqrt{2}$ |
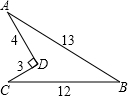 如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.
如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.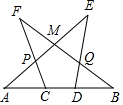 如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对.
如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对. 如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值.
如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值.