题目内容
3.某美食广场摊位(档口)出租给商户,采用统一物业管理,按照商户的日营业额收缴管理费,有一种摊位,如果经营商户的日营业额不低于1000元时,需上缴的管理费y(元)与商户当天的营业额x(元)成一次函数关系;如果日营业额低于1000元时,仍需缴管理费400元.一商户小王有两天的营业额分别是1000元、2600元,这两天分别上缴管理费400元,720元.根据以上信息,解决以下问题:
(1)请求出当x≥1000时,y与x之间的函数关系式;
(2)若小王某天的日营业额为2000元,求他应上缴的管理费;
(3)若小王有两天共上缴管理费1600元,请推断小王这两天营业额的最小值.
分析 (1)根据题意可以设出y与x之间的函数关系式,然后根据题目中的数据即可求得当x≥1000时,y与x之间的函数关系式;
(2)将x=2000代入(1)中的函数解析式即可解答本题;
(3)分两种进行讨论,即可解答本题.
解答 解:(1)设当x≥1000时,y与x之间的函数关系式是y=kx+b,
$\left\{\begin{array}{l}{1000k+b=400}\\{2600k+b=720}\end{array}\right.$,得$\left\{\begin{array}{l}{k=0.2}\\{b=200}\end{array}\right.$,
即当x≥1000时,y与x之间的函数关系式是y=0.2x+200;
(2)由题意可得,
将x=2000代入y=0.2x+200,得
y=0.2×2000+200=600,
即小王某天的日营业额为2000元,他应上缴的管理费是600元;
(3)由题意可知,
当两天中有一天的营业额不足1000元时,
则另一天的营业额为:1600-400=0.2x+200,得x=5000,
在此种请款下,当一天的营业额为零时,则这两天的营业额最小,最小是5000元,
当两天的营业额都不小于1000时,
设第一天的管理费为a元,则第二天的管理费为(1600-a)元,
则这两天的营业额为:$\frac{a-200}{0.2}+\frac{1600-a-200}{0.2}$=$\frac{a-200+1600-a-200}{0.2}=\frac{1200}{0.2}$=6000(元),
由上可得,小王这两天营业额的最小值是5000元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用一次函数的性质和分类讨论的数学思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.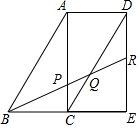 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )| A. | 3:1:2 | B. | 5:2:3 | C. | 4:1:3 | D. | 6:1:3 |
11.同时含有字母a,b,c,系数为1的6次单项式按以下规则排序:先看a的次数,a的次数高的单项式排在前面,若相同,再比较b的次数,最后比较c的次数,均是先高次后低次,则a2b3c排在第几位( )
| A. | 第4位 | B. | 第5位 | C. | 第6位 | D. | 第7位 |
18. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |
12.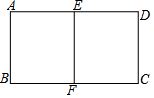 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )| A. | 2 | B. | $\frac{5}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
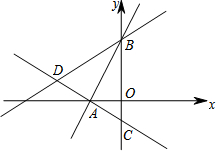 如图,在平面直角坐标系中,过点A的两条直线分别交y轴于B(0,3)、C(0,-1)两点,且∠ABC=30°,AC⊥AB于A.
如图,在平面直角坐标系中,过点A的两条直线分别交y轴于B(0,3)、C(0,-1)两点,且∠ABC=30°,AC⊥AB于A.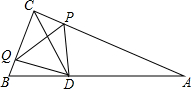 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD.