题目内容
18. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |
分析 直接利用直角三角形的性质进而得出CO,HO的长即可得出EH的长.
解答  解:连接CO,
解:连接CO,
∵正六边形ABCDEF,
∴∠BOC=60°,OB=OC,
∴△OBC是等边三角形,
此时AC⊥BE,
∵CH=6$\sqrt{3}$,
∴∠OCH=30°,
∴cos30°=$\frac{HC}{CO}$=$\frac{6\sqrt{3}}{CO}$=$\frac{\sqrt{3}}{2}$,
解得:CO=12,
故OH=6,
则EH=12,HO=6,
故EH=18.
故选:B.
点评 本题考查了正多边形和圆以及解直角三角形等知识,利用三角函数得出CO的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.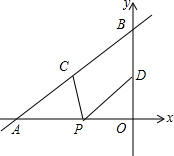 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |
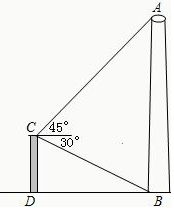 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4.
如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,CD=2.4,则点C到直线AB的距离等于2.4. 如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.
如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.