题目内容
14．
如图，E为等边△ABC的边BC上一点，∠CAE=∠CBD，AE=BD，求证：△CDE为等边三角形．
分析 利用等边△ABC的性质得出AC=BC，∠ACB=60°，证得△CAE≌△CBD，得出CE=CD，利用等边三角形的判定即可得出结论．
解答 证明：∵△ABC是等边三角形，
∴AC=BC，∠ACB=60°，
在△CAE和△CBD中，
$\left\{\begin{array}{l}{AC=BC}\\{∠CAE=∠CBD}\\{AE=BD}\end{array}\right.$，
∴△CAE≌△CBD，
∴CE=CD，∠DCB=∠ACB=60°，
∴△CDE为等边三角形．
点评 此题考查三角形全等的判定与性质，等边三角形的判定，掌握三角形的判定方法是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
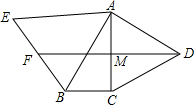如图，在△ABC中，∠ACB=90°，∠BAC=30°，△ABE和△ACD都是等边三角形，F是BE的中点，DF交AC于M，试说明线段AM与MC相等的理由．
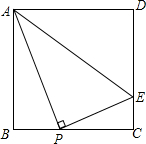如图，在正方形ABCD中，P是BC边上一点（不与点B，C重合），AP⊥PE．
y24-2×
=607．