题目内容
2.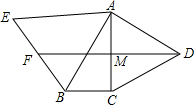 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,F是BE的中点,DF交AC于M,试说明线段AM与MC相等的理由.
分析 连接AF、FC,由等边三角形的性质可得AF是∠BAE的平分线,然后求出∠BAF=∠BAC=30°,再利用“角角边”证明△ABF和△ABC全等,由全等三角形对应边相等可得AF=AC,然后求出△AFC是等边三角形,再由等边三角形的性质求出AF=FC=CD=AD=AC,然后求出四边形AFCD是菱形,由菱形的对角线互相平分可得AM=MC.
解答 证明:连AF,FC,如图所示: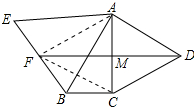
∵△ABE是等边三角形,F是BE的中点,
∴AF是∠BAE的平分线,
∴∠BAF=∠BAE=$\frac{1}{2}$×60°=30°,
∵∠BAC=30°,
∴∠BAF=∠BAC=30°,
在△ABF和△ABC中,
$\left\{\begin{array}{l}{∠BAF=∠BAC}&{\;}\\{∠AFB=∠ACB=90°}&{\;}\\{AB=AB}&{\;}\end{array}\right.$,
∴△ABF≌△ABC(AAS),
∴AF=AC,
∵∠FAC=∠BAF+∠BAC=30°+30°=60°,
∴△AFC是等边三角形,
又∵△ACD是等边三角形,
∴AF=FC=CD=AD=AC,
∴四边形AFCD是菱形,
∴AM=MC.
点评 本题考查了菱形的判定与性质、等边三角形的性质、全等三角形的判定与性质;作辅助线构造出全等三角形和菱形是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
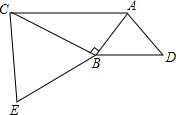 如图,△ABC中,∠ABC=90°,以AB、BC分别作等边△ABD和等边△BCE,求证:BD⊥CE.
如图,△ABC中,∠ABC=90°,以AB、BC分别作等边△ABD和等边△BCE,求证:BD⊥CE.
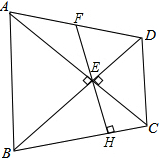 已知:△ABE和△DEC都是等腰直角三角形,∠AEB=∠DEC=90°,过E作EH⊥BC,交BC于H点,交AD于F点.当E是AC和BD的交点时,求证:
已知:△ABE和△DEC都是等腰直角三角形,∠AEB=∠DEC=90°,过E作EH⊥BC,交BC于H点,交AD于F点.当E是AC和BD的交点时,求证: 如图,△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{OE}{OB}$的值.
如图,△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,求$\frac{OE}{OB}$的值. 如图,E为等边△ABC的边BC上一点,∠CAE=∠CBD,AE=BD,求证:△CDE为等边三角形.
如图,E为等边△ABC的边BC上一点,∠CAE=∠CBD,AE=BD,求证:△CDE为等边三角形.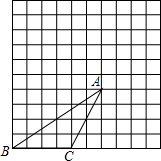 在如图所示10×10的方格中,有一个格点△ABC,请在图中画出两个格点△A1B1C1 和△A2B2C2,使△ABC∽△A1B1C1∽△A2B2C2(相似比不为1,且△A1B1C1为放大的三角形,△A2B2C2为缩小的三角形).
在如图所示10×10的方格中,有一个格点△ABC,请在图中画出两个格点△A1B1C1 和△A2B2C2,使△ABC∽△A1B1C1∽△A2B2C2(相似比不为1,且△A1B1C1为放大的三角形,△A2B2C2为缩小的三角形).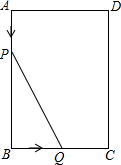 如图在矩形ABCD中,AB=8cm,Bc=6cm,动点P,Q分别从A,B向B、C运动,运动速度为1cm/s,当P、Q一点停止运动则另一点停止运动.设△PBQ的面积为y,点P、Q运动时间为x(s).
如图在矩形ABCD中,AB=8cm,Bc=6cm,动点P,Q分别从A,B向B、C运动,运动速度为1cm/s,当P、Q一点停止运动则另一点停止运动.设△PBQ的面积为y,点P、Q运动时间为x(s).