题目内容
9．已知a-b=2004，b-c=-2005，c-d=2007，则$\frac{（a-c）（b-d）}{a-d}$=$-\frac{1}{1003}$．分析 先根据a-b=2004，b-c=-2005，c-d=2007求得a-c=-1，b-d=2，a-d=2006，再将其代入分式求值即可．
解答 解：∵a-b=2004，b-c=-2005，c-d=2007，
∴（a-b）+（b-c）=2004+（-2005），（b-c）+（c-d）=-2005+2007，（a-b）+（b-c）+（c-d）=2004+（-2005）+2007，
即a-c=-1，b-d=2，a-d=2006．
∴原式=$\frac{（-1）×2}{2006}=-\frac{1}{1003}$．
点评 本题考查的是分式的化简求值，根据已知条件得出a-c=-1，b-d=2，a-d=2006是解答此题的关键．
练习册系列答案
相关题目
19．
| 多项式 | 多项式的项数 | 各项的系数 | 多项式的次数 |
| -2x+1 | 2 | -2，1 | 1 |
| x2-5x4+3 | 3 | 1，-5，3 | 4 |
| x2y+xy | 2 | 1，1 | 3 |
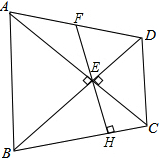已知：△ABE和△DEC都是等腰直角三角形，∠AEB=∠DEC=90°，过E作EH⊥BC，交BC于H点，交AD于F点．当E是AC和BD的交点时，求证：
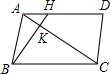如图，H为平行四边形ABCD中AD边上一点，且AH=$\frac{1}{2}$DH，AC和BH交于点K，求$\frac{AK}{KC}$的值．
如图，E为等边△ABC的边BC上一点，∠CAE=∠CBD，AE=BD，求证：△CDE为等边三角形．
四边形ABCD中，∠B=∠D=90°，AB=BC，AD=7，tanA=2，求CD的长．